Estabelecer uma fórmula para o cálculo do alongamento total de uma barra prismática, de comprimento e seção transversal com área , pendurada verticalmente por uma extremidade e sujeita à ação de seu próprio peso. (Supor o peso total da barra).
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos aqui uma barra prismática, de comprimento e seção transversal pendurada na vertical sob ação do seu próprio peso. Ressaltando, apenas sobre seu próprio peso!
Como o peso atua no centro da barra, temos o seguinte diagrama de equilíbrio:
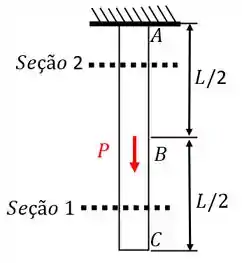
O objetivo aqui é calcularmos a deformação total da barra. Para isto, temos que utilizar a relação:
Isto é, precisamos somar as deformações de cada seção sob uma força uniforme (indicadas na nossa Figura).
Sendo assim, vamos aos cálculos!
Passo 2
Vamos começar pela seção 1, indicada na figura do Passo 1. Desenhando o diagrama de equilíbrio, temos:
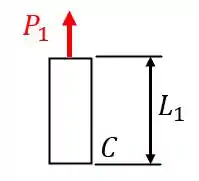
Portanto, como a barra está em equilíbrio , então, a força é igual a e a deformação devido a esta seção será:
Agora, basta repetirmos para a outra seção! Esboçando o diagrama de equilíbrio para a seção 2, temos:
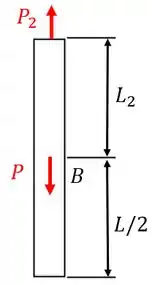
Como a barra está em equilíbrio , então, a força é igual a . Portanto, a deformação devido a esta seção será:
E então, a deformação total será:
E assim finalizamos a questão!