Um membro tracionado é composto de dois pedaços de material que são colados ao longo da linha . Por razões práticas, o ângulo é limitada à faixa de 0° a 60°. A tensão de cisalhamento permissível, , na junta colada é 3/4 da tensão de tração permissível . Qual deve ser o valor do ângulo , a fim de que a barra suporte o máximo de carga ? (Admitir que a resistência da junta colada controle o projeto.)

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

A questão aqui é o seguinte: qual o ângulo que conseguimos maximizar a força (tensão de tração )?

Vamos relembrar abaixo quais as tensões na seção inclinada

Para maximizarmos a força , é necessário que pelo menos uma das tensões acima seja a máxima possível ( ou ), ou até possivelmente ambos serem iguais!

Mas, temos que tomar muito cuidado. Precisamos determinar a maior força possível, mas que todo o conjunto da obra não falhe (ambas as tensões menores ou iguais ao limite)!

Então, a chave da questão consiste em igualar as tensões do plano inclinado e obter as seguintes funções: e . Plotando-as (basta fixar ), temos:

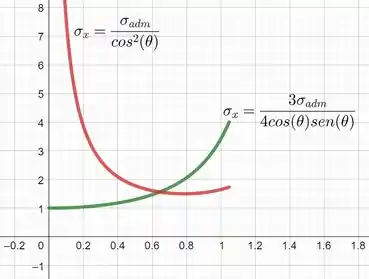
Para um mesmo valor de (que no gráfico está em radiano), temos dois valores possíveis de tensão. Para que o material não falhe, devemos escolher o valor de utilizando a curva abaixo.

Então, como o nosso objetivo é escolher o maior valor de , devemos escolher o valor de cuja coordenada , ou , da curva mais abaixo, seja o maior possível.

Com todos esses critérios, obtemos que o maior valor de será obtido quando ! E assim finalizamos a questão!