O pedestal visto na Fig. 1-8 está sujeito às cargas e . O comprimento da parte superior é igual a 500 mm e a seção transversal é quadrada com 75 mm de lado. A parte inferior tem e seção quadrada cujo lado é igual a 125 mm. Sabendo que , achar: (a) a deflexão do topo do pedestal; e (b) a relação entre as deformações axiais unitárias das partes superior e inferior.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Vamos começar relembrando a Figura 1-8 abaixo.
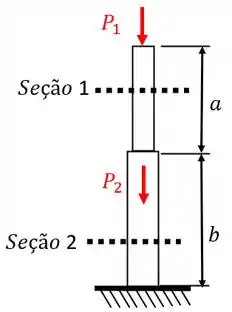
Como pode ser visto, ela está submetida a forças e em pontos específicos da nossa barra.
A questão nos pede duas informações. Na letra a), precisamos calcular a deformação total da barra, a qual é obtida a partir da seguinte relação:
Já na letra b), precisamos obter a relação entre as deformações axiais unitárias das partes superior e inferior. Aqui, vamos ter que assumir que e obter a seguinte relação .
Agora que já sabemos o que a questão pede, vamos para os cálculos!
Passo 2
Vamos começar resolvendo a letra a). Para calcularmos a deformação total da barra, vamos ter que obter a deformação de cada seção com distribuição constante de força (indicadas na Figura do Passo 1).
Portanto, neste caso, temos 2 seções. Começando pela seção 1, esboçando o seu diagrama de equilíbrio, temos:
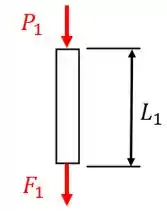
Sendo . Como a barra está em equilíbrio, temos que . Calculando a deformação devido a esta força, temos:
Agora, basta repetirmos para o procedimento para a seção 2! Esboçando o diagrama de equilíbrio para a seção 2, temos:
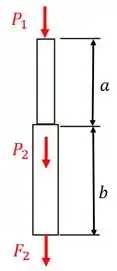
Sendo . Como a barra está em equilíbrio, temos que . Calculando a deformação devido a esta força, temos:
Portanto, a deformação total da barra será:
E assim finalizamos a letra a).
Passo 3
Para resolvermos a letra b), temos que fazer a razão assumindo que os comprimentos das barras são iguais. Isto é, .
Vamos aproveitar a obtenção das forças e do Passo 2 para desenvolver a nossa relação.
Sendo assim, a razão será:
E assim finalizamos a nossa questão!