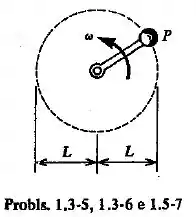
Um peso é suportado por um braço de comprimento que gira sobre um plano horizontal, sem atrito, em torno de um eixo vertical (ver a figura). A velocidade angular do peso e do braço é constante, . Desprezando o peso do braço, estabelecer a fórmula para o cálculo da área da seção transversal do braço, considerando uma tensão admissível, .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Uma questão que envolve movimento circular uniforme... Caramba, vamos precisar de um esforço um pouco maior para conseguir resolvê-la, mas nada de outro mundo.
Bom, queremos determinar aqui a fórmula para o cálculo da área transversal.
A questão nos pede para projetarmos o braço para que ele suporte uma tensão admissível . Portanto, temos:
Mas quem é esta força ? Esta é a pergunta que devemos responder agora.
Passo 2
Para podermos indicar quem é a força devemos lembrar um pouco da cinética. Considerando que o braço tem peso desprezível, temos o movimento circular uniforme de uma partícula de massa .
Para que ocorra o movimento circular, é necessário a existência de uma força centrífuga, na direção do centro do movimento até a partícula (a direção da barra)!
Em outras palavras, a força centrífuga é a força que causará uma tensão na nossa barra!
Então, lembrando lá da cinética, temos:
E portanto, a área da seção transversal é:
E assim finalizamos a questão!