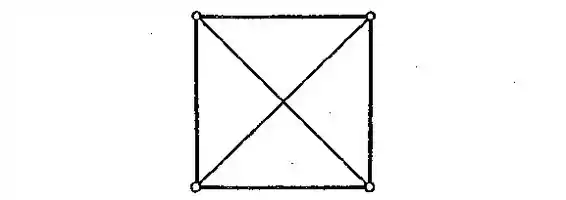
O quadro que se vê na figura é formado por barras externas de alumínio e diagonais em fios de aço . As áreas das seções transversais das barras de alumínio e dos fios de aço estão na relação 20:1. Achar as tensões nos fios de aço, se a temperatura do quadro aumentar de 45°C.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos um quadro, de forma quadrada, composto por barras externas de alumínio nos lados (comprimento ) e fios de aço nas diagonais (comprimento ).
A questão nos pede para determinarmos as tensões nos fios de aço após todo o quadro ser submetido a um aumento de temperatura de 45°C.
Como o alumínio tem um coeficiente de dilatação maior do que o aço, ao dilatarmos o quadro, deve-se surgir tensões compressivas no alumínio e tensões trativas no aço de forma que a deformação dos dois “sejam iguais”.
Isto é, devem surgir tensões que mantém as barras conectadas aos fios, mantendo assim o formato quadrado da estrutura.
Portanto, temos que trabalhar com duas vertentes: analisar a relação das deformações e analisar a relação das forças.
Passo 2
Vamos começar pela parte mais fácil. Vamos obter a relação entre as forças no fio e na barra.
Para isto, basta utilizarmos o método dos nós para qualquer dos vértices do quadro. Fazendo isto, teremos o seguinte diagrama de equilíbrio:
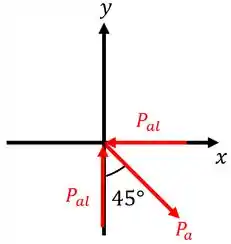
Portanto, utilizando as equações da estática, temos:
E assim conseguimos relacionar as duas forças!
Passo 3
Agora temos que relacionar a deformação das duas barras.
Como o fio permanece na diagonal do quadrado, a sua deformação será nesta mesma direção. Já as barras deformarão na direção horizontal e vertical.
Fazendo um esboço destes deslocamentos, temos:

Portanto, pelo Teorema de Pitágoras, temos:
Mas quem é e ? São as deformações devido a dilatação e a ação das forças em cada material! Portanto, substituindo as relações apropriadas, temos:
Lembrando, pelo enunciado da questão temos . Logo,
E assim finalizamos a questão!