Uma régua de aço fina cujas dimensões da seção reta são e de comprimento , é curvada por momentos aplicados nas extremidades, formando um arco circular com ângulo central de . Qual a tensão máxima na régua?
Passo 1
Nosso objetivo principal é determinar a máxima tensão. Pois muito bem! Sabemos que a fórmula da tensão é dada por:
E o raio da curvatura é calculado da seguinte maneira:
Como queremos o raio de curvatura, podemos definir como:
Agora, vamos fazer um esboço do que tá acontecendo! Pra ajudar a gente a entender melhor o problema...
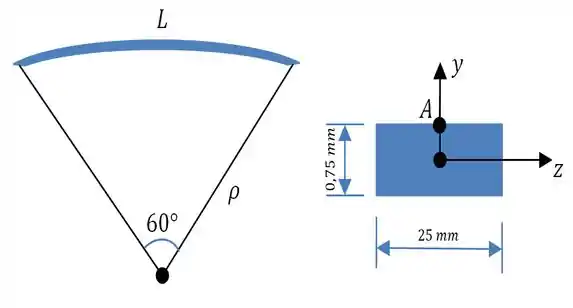
Isso aí em azul curvado é a nossa barra com e do lado a seção transversal dela. Sendo assim, o raio de curvatura vai ser dado usando a relação do arco de circunferência por...
Passo 2
Obtido o raio de curvatura, vamos obter o momento usando a fórmula abaixo...
E então, substituindo na fórmula da tensão...
Onde é a posição daquele ponto da figura...
Substituindo então, os valores numéricos...
Obtemos o valor da tensão máxima!