Resolver o Probl. 2.2-5 usando o círculo de Mohr.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Bom pessoal, como precisamos resolver a questão 2.2-5 utilizando o círculo de Mohr, precisamos então começar a questão relembrando o problema.
Na questão nós temos um elemento submetido ao estado plano de tensões e Com estes valores, (a) precisamos determinar as tensões em um elemento girado de um ângulo , (b) depois devemos localizar os planos de máxima tensão de cisalhamento e determinar essas tensões. E, por fim, (c) determinar o plano e as tensões tal que existe uma tensão normal nula.
Passo 2
Ufa, são muitas informações. Como esta é uma questão grande, vamos começar devagar. Vamos esboçar o círculo de Mohr e identificar as tensões quando .
Então, vamos começar pelo círculo de Mohr. A sua equação será:
Sendo e . Portanto,
Esboçando o círculo com o estado inicial juntamente do estado do elemento após rotação temos:
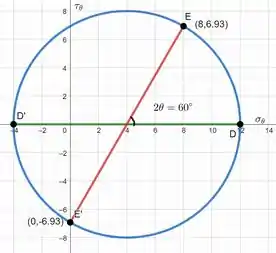
Como queremos uma rotação de 30° no sentido horário, no círculo temos que rotacionar também no sentido horário.
Ao encontrarmos a interseção da reta rotacionada com o círculo teremos o nosso estado de tensões. Neste caso, ele será:
E assim terminamos a letra a).
Passo 3
Agora vamos para a letra b). Aqui nós precisamos determinar os planos de máxima tensão de cisalhamento e os valores dessas tensões.
Então, esboçando o círculo de Mohr, temos:
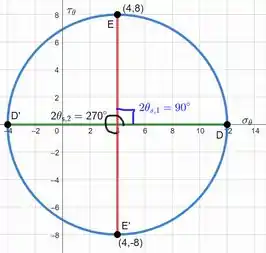
E por fim, conseguimos identificar que os planos são obtidos por uma rotação de e . Já as tensões relativas a esse estado são:
Passo 4
Já para a letra c) nós não temos trabalho nenhum! O objetivo aqui é identificar um plano tal que existe uma tensão normal nula e identificar os valores das outras tensões.
Entretanto, para a nossa alegria, este plano já foi identificado na letra a) da questão, sendo resolvida no Passo 2!
E assim conseguimos terminar a letra c) sem ter que fazer conta alguma!
Por fim, assim finalizamos a questão!
Resposta
- Os planos de tensão cisalhante máxima são obtidos de uma rotação e . As tensões relativas a esses planos são:
- A tensão normal em um plano é igual a zero quando . O esboço do elemento é: