Resolver o problema anterior, agora considerando o peso do braço. (Supor que o material do braço tenha o peso específico )
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
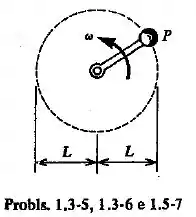
Bom pessoal, esta questão é basicamente uma continuação da questão 1.3-5. A diferença é que, além da força centrífuga da partícula de peso na extremidade do braço, a qual foi:
Teremos também uma força centrífuga devido a barra (agora que tem massa a gente tem que considerar essa força).
Mas e agora, como calcular a força centrífuga de um corpo rígido? Bom, para facilitar isto, basta considerarmos o corpo rígido como uma partícula de pesos iguais e localizada no centro de massa da barra (meio da barra).
Esta é a única diferença. Basta somarmos ambas as forças e repetirmos o procedimento que fizemos na questão anterior.
Passo 2
Agora que já entendemos o que devemos fazer nesta questão, vamos calcular a força centrífuga devido a barra.
Sabemos que a massa está localizada a uma distância . Já a massa nós temos que correlacionar com o peso específico . Portanto, temos:
E portanto, a força centrífuga devido a barra é:
Passo 3
Após descobrirmos qual a força centrífuga devido a massa da barra, podemos calcular a força centrífuga total. Ela será:
Portanto, a área da seção transversal será:
E assim finalizamos a questão!