Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 5.5 - Ex. 2

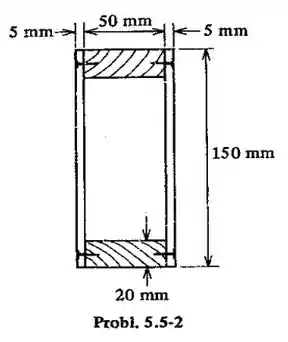
Uma viga, tipo caixa, de madeira, com laterais de madeira compensada, tem as dimensões da seção reta mostrada na figura. O compensado é fixado às bases por meio de pregos que tem capacidade para suportar uma carga admissível de 10,0   k g f em cisalhamento. Achar o espaçamento (passo) admissível entre os pregos, nas seções onde a força cortante é de 50   k g f e 100   k g f .

Passo 1

Fala galerinha! Questãozinha nova na área!

Analisando o enunciado, podemos extrair os seguintes dados

V = 50   k g f / 100   k g f

  F p r e g o = 10,0   k g f

A questão pede o espaçamento (passo) admissível entre os pregos, nas seções onde a força cortante é de 50   k g f e 100   k g f . Aqui vai um esboço do problema pra entender mais ou menos o que está acontecendo

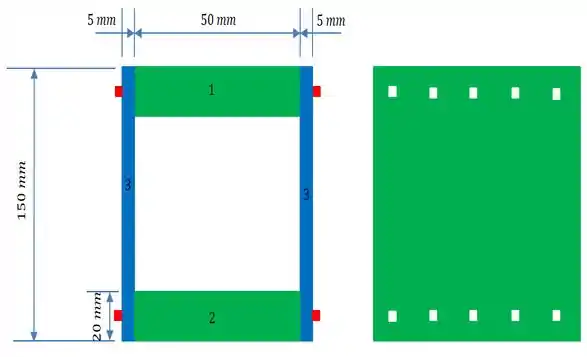
Passo 2

Começamos calculando o centroide y C . Para isso, vamos separar a seção transversal da viga em quatro retângulos...

y c = ∑ A ⋅ y ∑ A

y c = 2 A 3 y 3 + A 2 y 2 + A 1 y 1 2 A 3 + A 2 + A 1

y c = 2 ⋅ 150 ⋅ 5 ⋅ 75 + 50 ⋅ 20 ⋅ 140 + 50 ⋅ 20 ⋅ 10 2 ⋅ 15 0 ⋅ 5 + 2 ⋅ 50 ⋅ 2 0

y c = 75   m m

Passo 3

Agora calculamos o momento de inércia de toda a seção transversal em relação ao centroide

I = 2 I 3 + I 2 + I 1

I = 2 ⋅ 5 ⋅ 15 0 3 12 + 2 50 ⋅ 2 0 3 12 + 50 ⋅ 20 ⋅ 65

I = 3009166,67   m m 4

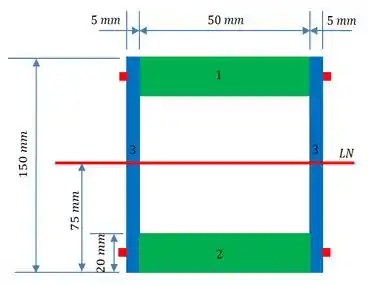
Passo 4

Agora vamos escolher e calcular o momento estático. Existem várias formas de calcular o momento estático. Vamos escolher a parte 1:

Q = 50 ⋅ 2 0 ⋅ 65

Q = 65000   m m 3

Passo 5

Bom! Agora vem a parte derradeira!

Há um espaçamento s entre os parafusos, e que à medida que o fluxo de cisalhamento avança sobre a área que foi escolhida pro momento estático, ele gera um cisalhamento em dois parafusos. Essa relação é dada dessa forma:

q = 2 F p a r a f u s o s

O número dois aparece na equação acima, pois o fluxo resiste a 2 pregos simultaneamente.

Por outro lado, a fórmula para o fluxo de cisalhamento é

q = V Q I

Igualando as duas equações:

V Q I = 2 F p a r a f u s o s

Isolando s :

s = 2 F p a r a f u s o I V Q

E substituindo os dados que nos foram fornecidos. Para a força cortante de 50   k g f , temos que...

s = 2 ( 10,0   k g f ) ( 3009166,67   m m 4 ) ( 50   k g f ) ( 65000   m m 3 )

s = 35   m m

E para a força cortante de 100   k g f :

s ' = 2 ( 10,0   k g f ) ( 3009166,67   m m 4 ) ( 10 0   k g f ) ( 65000   m m 3 )

s ' = 70   m m

Resposta

35   m m   e   70   m m

Ver Outros Exercícios desse livro