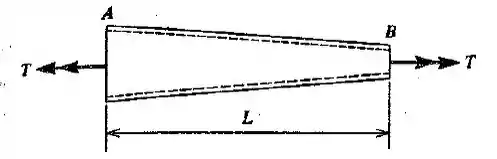
Um tubo cônico de seção transversal circular, de parede fina e longo (ver a figura), é sujeito a um torque . O tubo tem espessura de parede constante e comprimento . Os diâmetros médios das seções retas nas extremidades e são e , respectivamente. Deduzir uma fórmula para o ângulo de torção, , do tubo.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos deduzir o ângulo de torção de um tubo cônico de parede fina.
O princípio por trás é fácil. O difícil mesmo serão as contas, bem trabalhosas!
Mas vamos devagar que vai dar tudo certo! Vamos começar escrevendo a fórmula para calcularmos o ângulo . Ela será:
Só que o momento de inércia é expresso por:
Então, a nossa integral será:
Passo 2
Agora basta resolvermos a nossa integral. Portanto,
E assim finalizamos a questão.