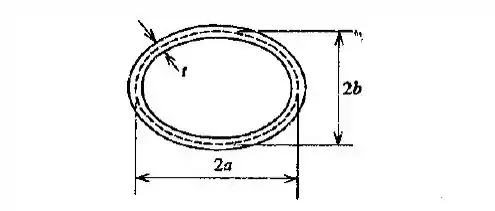
Um tubo fino, tendo uma seção transversal elíptica (ver a figura), é sujeito a um torque . Determinar a tensão de cisalhamento, , e o ângulo de torção por unidade de comprimento, , se ; ; ; . (Nota. A área de uma elipse é e sua circunferência é aproximadamente )
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos calcular a tensão de cisalhamento e o ângulo de torção por unidade de comprimento . Apesar de termos uma tubulação de geometria diferente, não precisamos nos assustar!
Vamos começar calculando a tensão cisalhante. Para isto, temos a seguinte fórmula:
Sendo que é a área delimitada pela linha tracejada. Neste caso, temos . Então,
E assim calculamos a tensão cisalhante! Percebam só que o torque tem que ser escrito em , e no enunciado foi dado em !
Passo 2
Para finalizarmos a questão temos que calcular o ângulo de torção . Para isto temos:
Sendo sendo o comprimento da circunferência, que é dado por . Portanto,
E assim finalizamos a questão!