Um tubo vazado, , encaixa-se na extremidade de uma barra, , como mostrado na figura. Existe um furo na barra que faz um ângulo com uma linha que passa por dois furos na barra . A barra é, então, torcida até que os furos fiquem alinhados, e um pino seja colocado através deles. Quando o sistema retorna ao equilíbrio estático, qual é a energia de deformação total das duas barras? (Admita e representando os momentos de inércia polar das barras e , respectivamente. O módulo de elasticidade transversal é o mesmo para as duas barras.)
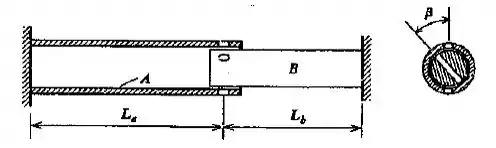
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos calcular a energia de deformação das duas barras conforme mostrada o enunciado do problema.
Nosso primeiro passo é determinar o torque ao qual as duas barras estão submetidas. Para isto, basta usarmos a lei da ação e reação. Ele nos diz que os torques atuantes em ambas as barras são iguais em módulo.
Agora que a gente sabe como se comporta o torque, temos que encontrar uma relação para ela com o ângulo de deformação . E esta relação é tal que:
Isto é, a deformação angular total das duas barras deve ser igual ao desnível inicial !
Desenvolvendo esta relação agora, teremos:
Passo 2
Agora já podemos calcular a energia de deformação. Para isto, precisamos lembrar da seguinte relação:
Só que a nossa barra consiste em duas barras distintas. Sendo assim, temos que somar a energia de deformação das duas seções. Logo,
E assim a gente finaliza a questão!