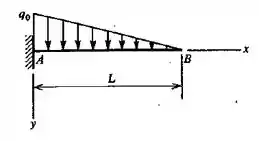
Uma viga em balanço suporta uma carga triangular como se vê na figura. Obter as fórmulas para a deflexão e o deslocamento angular na extremidade livre.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar a equação da linha elástica, como também a deflexão e o deslocamento angular , para uma viga engastada submetida a um carregamento triangular.
Já que estamos falando do carregamento, vamos aproveitar para obter a sua equação! Ela será:
Agora a gente vai ter um trabalhinho razoável, pois, podemos relacionar a equação da linha elástica com o carregamento através da seguinte relação:
Portanto, vamos ter que integrar a equação do carregamento quatro vezes!!! E ainda aplicar as condições de contorno...
Então, vamos as contas!
Passo 2
Agora que a gente já conhece o nosso carregamento, vamos aproveitar para fazer integrações sucessivas (até determinarmos a equação da linha elástica). Portanto,
E assim acabamos a parte de integração da nossa equação!
Passo 3
Agora temos que identificar cada uma das quatro incógnitas. E para isto, precisaremos de condições de contorno.
As primeiras condições que vamos aplicar para esta viga é a deflexão e inclinação nula no engastamento. Isto é, . Portanto,
Como ainda temos duas incógnitas, precisamos de duas condições de contorno. E elas são e . Portanto,
Então, temos e . Portanto, a equação da linha elástica é:
E assim chegamos a nossa equação da linha elástica!
Passo 4
Para finalizarmos a questão, temos que descobrir a equação da deflexão e do deslocamento angular em . Portanto, a deflexão será:
Já o deslocamento angular será:
E assim finalizamos a questão!