Uma viga com extremidades em balanço (ver a figura) suporta uma carga uniforme de intensidade em cada balanço. Admitindo que a viga seja um perfil com , determinar a tensão normal máxima na viga e a deflexão para cima, , no meio da viga.
Passo 1
Nosso objetivo principal é determinar a tensão normal máxima na viga e a deflexão para cima, , no meio da viga.
Pois muito bem! Sabemos que a fórmula da tensão é dada por:
Onde...
- é o momento fletor em uma seção transversal da viga;
- é a posição do ponto da seção
- é o momento de inércia da área da seção
Lembrando que dependendo dos sinais de e de , a tensão pode assumir valores positivos ou negativos, de tração ou de compressão.
Passo 2
Agora, vamos voltar nossa atenção pra obtenção dos diagramas de esforço cortante e momento fletor da viga. Por isso, façamos um esboço do diagrama de corpo livre...
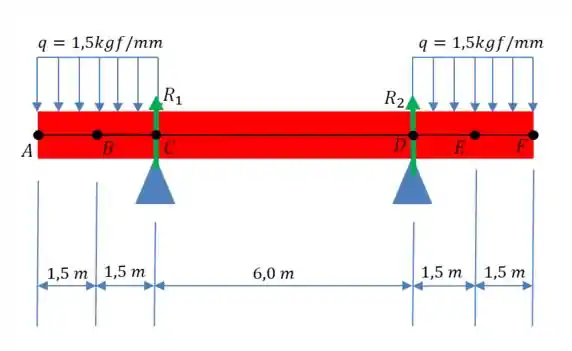
Como nossa barra é simétrica, temos que...
De boinhas, né? Bora lá, então! Vamos dividir a viga em três seções específicas pra determinar nossa momento fletor...
- Seção
- Seção
- Seção
Começando pela seção , temos que...
Para a seção , temos que...
E finalmente para a seção , temos que...
Chegamos assim, até o seguinte diagrama de momento fletor...
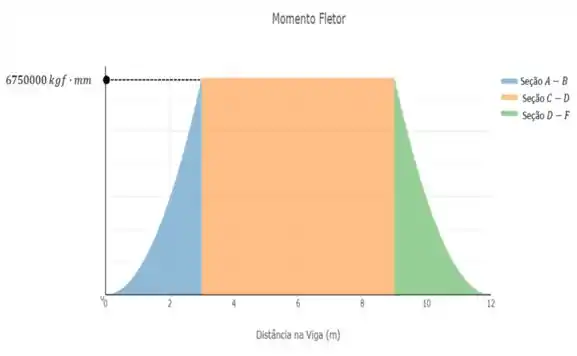
Onde podemos ver que o módulo do momento fletor máximo na viga é...
Passo 3
Obtido o momento máximo, vamos dar uma olhada na tabela com as vigas do tipo ...
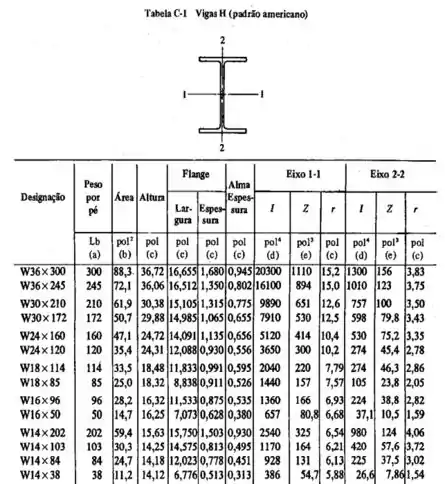
Com base nela podemos extrair os outros dois dados que faltam na fórmula abaixo...
Que são o e o valor do ! Pela tabela, temos que...
Logo, a tensão máxima vai ser dada por...
Passo 4
Agora, vamos atrás da deflexão! Representando aquela força distribuída do enunciado como se fosse apenas uma força comum, obtemos a seguinte figura, onde está esquematizada a deflexão ...
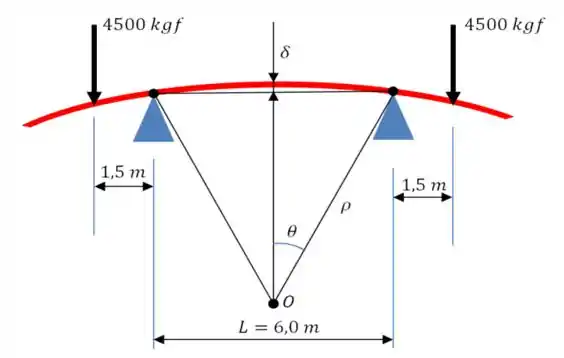
E como podemos ver aí em cima, vai ser dada por...
Onde é um ângulo pequeno, geralmente dado pela seguinte fórmula...
E o raio de curvatura, a gente já sabe que a fórmula dele é dada por...
Onde é aquele momento máximo lá que a gente já tinha determinado no :
Sendo assim;
Então, calculando :
Temos que o valor de vai ser igual à...
O gabarito do livro na tensão máxima deu , mas aparentemente está errado, tanto que o produto pegou aqui os mesmos valores pra obter a deflexão e achou o valor certo para !
Show!?