Uma viga simples, com vão , suporta uma carga uniforme de intensidade . Calcular a tensão de flexão máxima, caso a viga tenha seção reta retangular com largura e altura .
Passo 1
Nosso objetivo principal é determinar a tensão de flexão máxima na viga, !
Pois muito bem! Sabemos que a fórmula da tensão é dada por:
Onde...
- é o momento fletor em uma seção transversal da viga;
- é a posição do ponto da seção mais distante possível do centroide. Isso na caso da tensão admissível.
- é o momento de inércia da área da seção
Lembrando que dependendo dos sinais de e de , a tensão pode assumir valores positivos ou negativos, de tração ou de compressão.
Vamos começar então, fazendo um esboço do diagrama de corpo livre dessa viga...
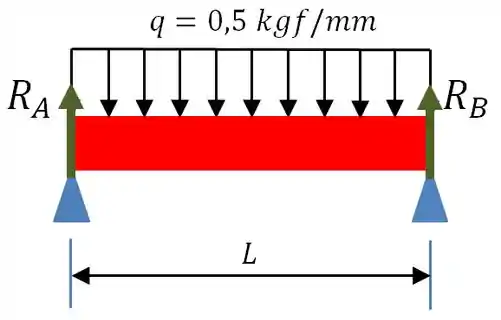
Passo 2
Com base na figura acima, por simetria, temos que...
Agora, baseado nesses dados, vamos obter o momento fletor e esforço cortantes atuantes na barra.
Primeiro calculemos o esforço cortante...
E depois, o momento fletor...
Temos então, o seguinte gráfico de momento fletor...
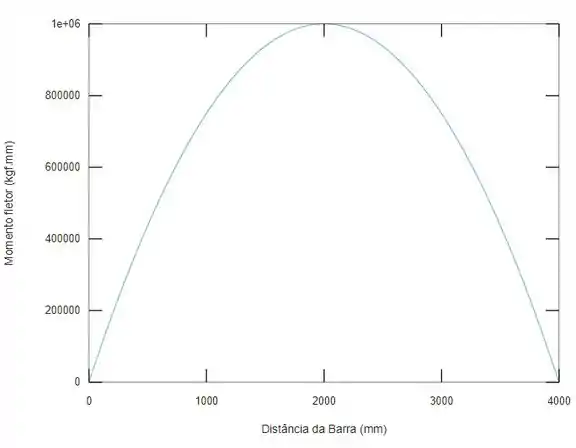
E como podemos ver aí, o momento máximo ocorre em ou . E ele vai valer...
Passo 3
E a gente sabe que a nossa viga tem uma seção reta retangular com largura e altura . Sendo assim, fica de boas calcular o momento de inércia ...
E a posição mais distante que nos garante a tensão máxima, vai ser a metade da altura da seção... Ou seja;
Sendo assim, podemos obter :