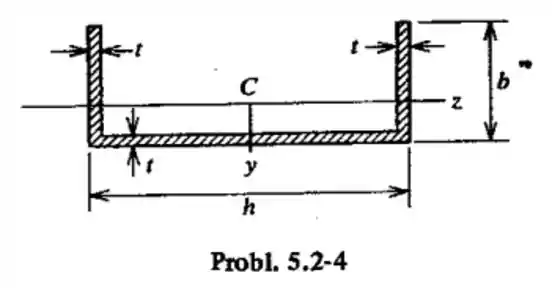
Uma viga de seção reta em forma de é sujeita a um momento fletor em relação ao eixo . Qual deve ser a espessura, , de maneira que as tensões na flexão no topo e na base do perfil estejam na razão , sendo e ?
Passo 1
Vamos começar!
O que nós sabemos?
Sabemos que a força na viga vai gerar nela esforços internos na forma de forças cortantes e momentos fletores .
Esses momentos fletores vão gerar na viga tensões normais de flexão , de acordo com a fórmula da flexão:
Onde:
- (ou só “”) é o momento fletor em uma seção transversal da viga;
- é a posição do ponto da seção em que se quer calcular a tensão em relação à linha neutra da seção;
- & (ou só “”) é o momento de inércia da área da seção.
Lembrando que nessa equação, dependendo dos sinais de e de , a tensão pode assumir valores positivos (de tração) ou negativos (de compressão).
Beleza!
E o que é que está acontecendo no exercício?
Nesse exercício, vamos ter certas seções da viga onde o momento fletor vai ter os seus “valores críticos”: os seus maiores valores positivo e negativo.
Nessas seções, que vamos chamar de “seções críticas”, há a chance de que a tensão normal atinja, ou no topo ou na base da seção, o seu valor máximo em tração ():
...e/ou o seu valor máximo em compressão ():
...sendo que, para a viga do exercício, essas tensões tem que estar numa razão de para . Ou seja, essas tensões tem que satisfazer as condições:
E o que é que o exercício quer?
Ele quer que a gente determine a espessura , de tal forma que as condições acima ainda sejam respeitadas.
Então, para resolver esse exercício, vamos ter que:
1. Encontrar os momentos fletores críticos na viga em função de .
Para tanto, podemos aplicar os métodos da estática: DCL, equilíbrio, análise dos esforços internos & diagramas de esforços internos.
2. Analisar a geometria em da seção transversal da viga para encontrar a posição de sua linha neutra e o seu momento de inércia da área .
3. Definir os “valores críticos” de para a viga e aplicar a fórmula da flexão usando esses valores e os momentos fletores críticos encontrados anteriormente.
Assim, vamos encontrar as tensões máximas de tração () e compressão () na viga
E, finalmente, 4. Aplicar as condições na razão dada de
Assim, vamos descobrir o valor de !
Passo 2
Então vamos começar encontrando os momentos fletores críticos na viga através dos métodos da estática!
O exercício não nos disse nada sobre o momento fletor! Então, vamos supor que ele vai ser dado por uma letra ...
Passo 3
Agora, podemos seguir para o estudo das propriedades geométricas da seção transversal dessa viga, começando pela determinação da:
![]()
Para calcular essa posição, devemos observar a geometria da seção da viga:
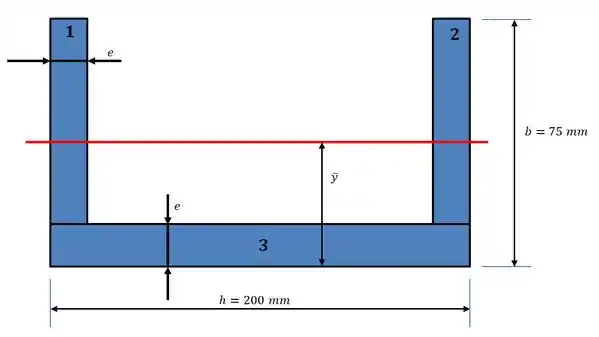
Com isso, podemos finalmente calcular a posição da linha neutra usando a fórmula:
Que é a posição da nossa linha neutra!
Passo 4
Depois da posição da linha neutra, podemos calcular para a seção da nossa viga o:
![]()
Aqui, devemos começar calculando o momento de inércia da área de cada elemento.
No nosso caso, tanto o elemento quanto o elemento tem o mesmo momento de inércia.
Dessa forma, os dois vão ter momentos de inércia da área dados pela fórmula .
Assim, para o elemento e que estão em pé com uma base e uma altura , vamos ter que:
Já para o elemento , que está deitado com uma base uma altura , vamos ter que:
E calculando tudo, vamos encontrar que:
Passo 5
Agora, podemos definir os “valores críticos” (máximos positivo e negativo) de para essa viga.
Assim, vamos poder aplicar a fórmula da flexão usando esses valores e o valor crítico de encontrados lá no passo .
Então vamos lá!
Em qualquer viga, os valores máximos positivo e negativo de vão acontecer para o topo e para a base da viga.
Para a nossa viga:
Isso significa que o valor máximo positivo da posição de um ponto dessa seção em relação à sua linha neutra vai ser:
E que o valor mínimo negativo da posição de um ponto dessa seção em relação à sua linha neutra vai ser:
Passo 6
Com esses valores, temos que as tensões na base e no topo vão valer...
Como temos que ter o seguinte...
Então, ficamos com...
Tirando a raiz...
Obtemos o seguinte resultado...
Pronto! Finalizamos aqui! Até a próxima!