Uma viga de madeira, de seção reta quadrada de , é carregada e apoiada como se vê na Fig 5-5. Determinar a carga admissível, , e a deflexão, , no meio do vão, sendo ; ; , e a tensão admissível máxima na viga for .
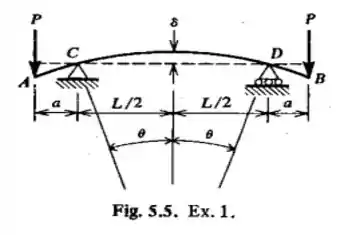
Passo 1
Nosso objetivo principal é determinar a carga admissível, , e a deflexão , no meio do vão.
Pois muito bem! Sabemos que a fórmula da tensão é dada por:
E o raio da curvatura é calculado da seguinte maneira:
Como queremos o raio de curvatura, podemos definir como:
Bom! A parte da viga entre os suportes está sob flexão pura! Em relação ao apoio , está sendo gerado um momento igual à...
Passo 2
Sendo assim, uma vez que a tensão admissível máxima na viga é , podemos determinar o valor de ...
Como a barra é quadrada, vai ser metade do lado, ou seja
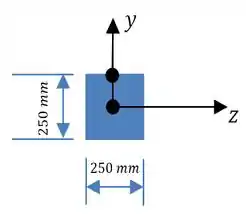
Substituindo então, os valores numéricos...
Passo 3
Agora vamos atrás da deflexão!
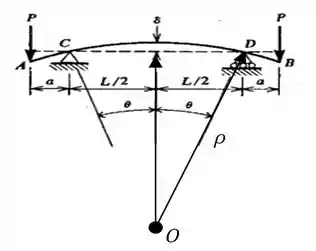
Bem! Pela figura acima, podemos ver que vai ser dado por...
Onde é um ângulo pequeno, geralmente igual à...
E o é dado por...
Substituindo isso na fórmula do ...
Pronto! Missão cumprida! Achamos o !
Terminamos aqui!