Enunciado
Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 5.8 - Ex. 5
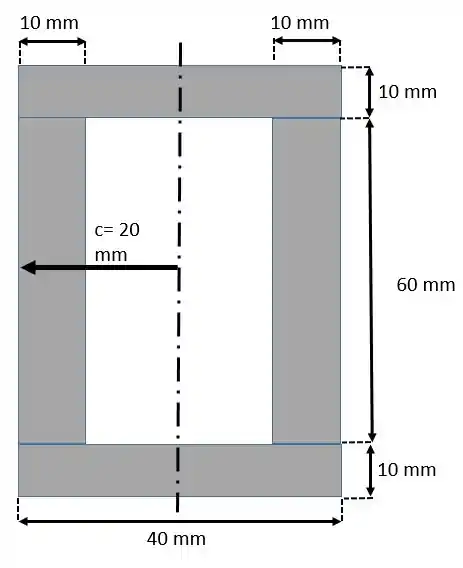
Uma viga simples, de vão suporta uma carga uniforme de . A seção reta da viga é mostrada na figura. Qual a espessura necessária das chapas de aço, se as tensões admissíveis forem para o aço e para a madeira. Considerar que os módulos de elasticidade para o aço e para a madeira são e , respectivamente.
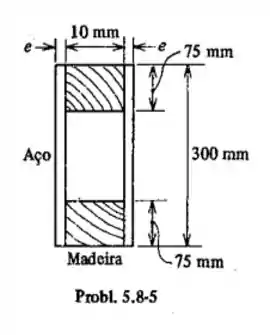
Passo 1
O problema pede o maior momento fletor permissível, que é dado pela equação:
Ou
Onde:
- é a tensão normal admissível.
- é o momento fletor.
- o momento de inércia.
- a maior distância entre a linha neutra e um ponto da peça.
Porém, além de ter que utilizar essa equação temos uma peça formada por dois materiais diferentes e para isso vamos ter que achar a seção transformada. Posteriormente, vamos poder utilizar a nossa equação do momento fletor tranquilamente.
Então vamos lá!
Passo 2
O cálculo da seção transformada é feito da seguinte maneira, sabendo que a viga é encurvada no eixo vertical. Originalmente temos:
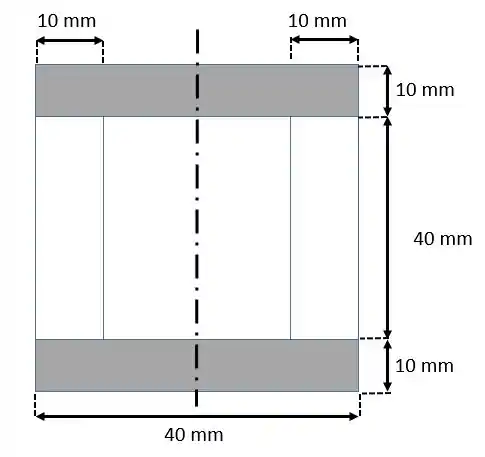
Observe que a linha central (com traços e pontos) está representando o eixo por onde a a viga é encurvada.
Agora vamos transformar essa peça em uma outra equivalente e toda feita de alumínio. Fazemos isso por meio de uma relação da forma:
Presta atenção agora! Vamos pegar as dimensões da peça de latão que são paralelas ao eixo e multiplicar pelo fator . Obtendo a seção transformada:
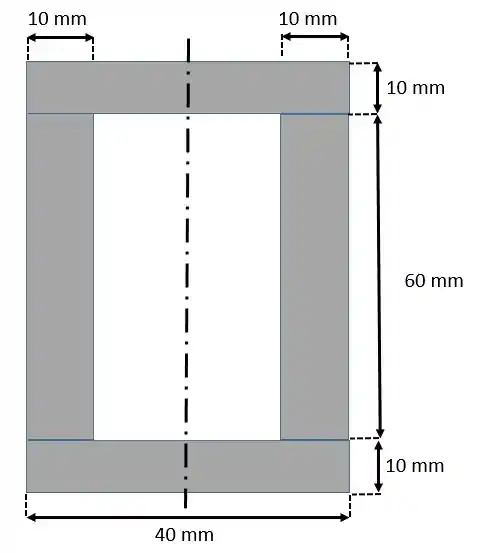
Pronto! Temos a seção transformada (toda em alumínio no caso). Agora vamos calcular o momento de inércia desta seção no passo 3.
Passo 3
O momento de inércia é calculado normalmente, para seções retangulares, da forma:
Neste caso vamos calcular o momento de inércia do retângulo grande de dimensão () e subtrair do pequeno de dimensão ().
Mas a gente tem que lembrar que o eixo agora é vertical então a base esta na vertical e a altura na horizontal, ok!?
Passo 4
Agora é só jogar na equação do momento fletor e pronto!
Observe que a distância é a maior distância entre o eixo e a peça!
