Uma amostra de dez casais e seus respectivos salários anuais (em s.m.) foi colhida num certo bairro conforme vemos na tabela abaixo:
Sabe-se que:
![]()
- Calcule a média e o desvio padrão do salário anual dos homens.
- Calcule o primeiro, segundo e terceiro quartis do salário anual das mulheres.
- Construa o diagrama de dispersão e encontre a correlação entre o salário anual dos homens e o das mulheres. O que os resultados indicam?
Passo 1
(a)
Pra calcular a média e o desvio padrão, só vamos aplicar fórmulas.
Como: e .
Passo 2
Pra variância...
A gente já conhece todos esses valores, até o que a gente acabou de calcular.
Daí:
Passo 3
(b)
Primeiro colocamos os salários das mulheres em ordem crescente...
Muito importante fazer isso, se não fica tudo errado... não esquece!!
Daí agora é só localizar os quantis e achar o valor referente...
O segundo quantil , que é a mediana, fica no meio, na posição:
Como ... o segundo quantil é o valor na posição (média entre o quinto e o sexto).
Passo 4
O primeiro quantil , fica na posição:
Uma média ponderada entre o terceiro e o quarto valor.
Já o fica na posição:
Média ponderada entre o sétimo e o oitavo.
Passo 5
(c)
O diagrama de dispersão é fácil, só plotar os dados dos homens e das mulheres, um em cada eixo.
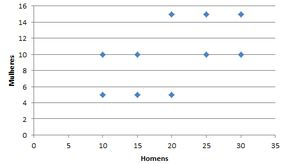
Passo 6
Vamos achar a correlação agora, que é:
Temos muito o que calcular antes então.
O a gente já conhece da letra (a), é o desvio padrão dos homens.
Vamos calcular o das mulheres.
Onde:
E daí:
Passo 7
Falta só que é pela fórmula:
Substituindo tudo:
Passo 8
Agora que já temos tudo, é só juntar e achar a correlação.
Essa correlação indica uma relação linear positiva (quando um cresce o outro cresce também) moderada entre o salário dos homens e suas respectivas mulheres.
Resposta
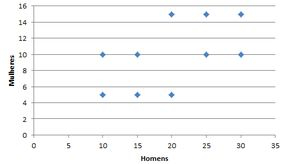
Essa correlação indica uma relação linear positiva (quando um cresce o outro cresce também) moderada entre o salário dos homens e suas respectivas mulheres.