Limites

Fala aí, bem vindo ao RespondeAí! No nosso site você encontra todo o conteúdo necessário para mandar bem na sua prova de Cálculo na faculdade.

Pra entender limites, é bom começar pensando em um gráfico. Da uma olhadinha aqui nessa curva normal:

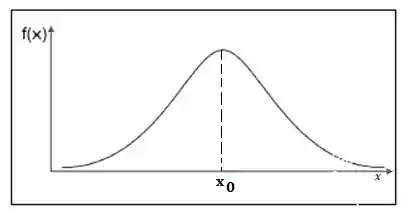
Observando essa curva, pense um pouco no que acontece a medida que vamos aumentado o valor de . Perto de a curva atinge seu ponto máximo. E o que acontece se a gente aumentar o valor de ? A curva vai diminuído e ficando cada vez mais próxima de zero, mas nunca atinge o valor zero, não é mesmo?! E se o valor de for um bilhão? e se for um trilhão? e se for um quadrilhão? Nesse caso o valor da curva vai ser muito, muito, pequeno, mas ainda sim não será zero!

Mas e se o valor for tão grande que chega próximo do infinito? Então nesse caso, a curva vai estar tão proxima de zero, que é praticamente indistinguível. Aprender Limites envolve além de aprender de um novo conceito: de que as vezes as coisas estão tão próximas que podem ser consideradas quase iguais.

Para expressar isso em simbologia matemática a gente faz assim:

e a gente ler assim: o limite da função quando tende ao infinito!

Como podemos observar no gráfico da função normal, quando mais o cresce mais próximo de parece ficar a função . Mas é importante ressaltar que ela nunca toca o eixo , então por isso dizemos que o limite da função Normal quando tente a infinito é :

Então vamos pensar em outro exemplo simples. Se então:

Mas o que é um limite? Pra que eu vou usar limite

Um limite é uma operação matemática que ao invés de calcular o valor de vai calcular o valor da função quando estamos próximos de .

Uma das principais utilidades dos limites é estudar condições matemáticas consideradas impossíveis. Por exemplo, qual é a solução no seguinte caso:

De cara, você pode dizer que não tem resposta! Afinal, a gente aprendeu que é impossível dividir por zero! Mas é exatamente em situações como essa em que aplicamos os conceitos de limites.

Ao invés de pensar em , e se a gente pensar , e depois em , e depois em e indo pra valores cada vez menores, valores tão infinitesimalmente pequenos que eles tendem a zero. Perceba que a gente não vai calcular , a gente vai calcular quando é quase zero.

A gente chama isso de “o limite da função tendendo a zero”, e escrevemos assim:

É em situações como essa em que a gente aplica os conceitos de limite.

Então, se a gente olhar o gráfico da função vamos ver que a medida que vamos chegando perto de o valor de vai ficando cada vez maior, e essa tendência continua, e quanto mais perto fica de zero, mais perto o vai ficando do infinito.

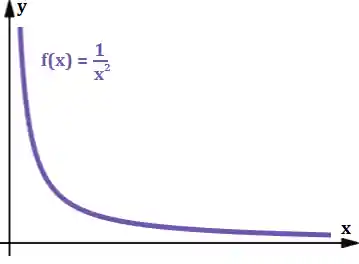
Então a gente pode dizer que o “o limite da função com tendendo a zero é infinito”

Viu só que da hora?! Os limites são uma ferramenta tão maneira que permite coisas impossíveis!

Vamos fazer um exercício para deixar o conceito inicial de Limites mais claro, mas depois você pode conferir nosso Raio-X do assunto e verificar todos os capítulos e tópicos que temos no nosso site

Exercício

Vou deixar vocês com um exercício do tópico de Introdução a Limites, onde o nosso Expert usa algumas propriedades de Limites para calcular o seguinte limite

Se achou que as coisas estão complicadas demais, confere aqui em baixo nosso Raio-X que serve como guia para você aprender tudo de Limites!