Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 9.Estatísticas Reais - Ex. 1

Analisando os dados

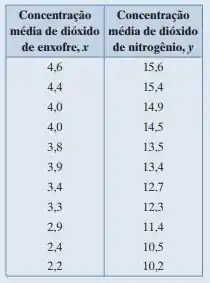
(a) Os dados na Tabela 9.19 mostram as concentrações médias de dióxido de enxofre (em partes por bilhão) e de dióxido de nitrogênio (em partes por bilhão) em 11 anos. Construa um diagrama de dispersão e conclua sobre o tipo de correlação entre as concentrações médias de dióxido de enxofre e dióxido de nitrogênio.

(b) Calcule o coeficiente de correlação r e verifique sua conclusão na parte (a).

(c) Teste a significância do coeficiente de correlação encontrado na parte (b). Use a = 0,05.

(d) Determine a equação da reta de regressão para as concentrações médias de dióxido de enxofre e dióxido de nitrogênio. Adicione o gráfico da reta de regressão ao seu diagrama de dispersão na parte (a). A reta de regressão parece ser um bom ajuste?

(e) Você pode usar a equação da reta de regressão para prever a concentração média de dióxido de nitrogênio dada a concentração média de dióxido de enxofre? Por quê, ou por que não?

(f) Encontre o coeficiente de determinação r2 e o erro padrão da estimativa se. Interprete seus resultados.

Passo 1

Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?

(a) Usando o software Excel e a partir dos dados informados, obtemos o seguinte diagrama de dispersão:

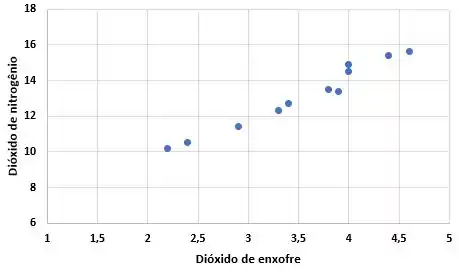
O gráfico de dispersão se inclina para cima, portanto, podemos afirmar que os dados têm uma correlação linear positiva.

(b) Com auxílio do software Excel, e com os dados do enunciado construímos a tabela a seguir:

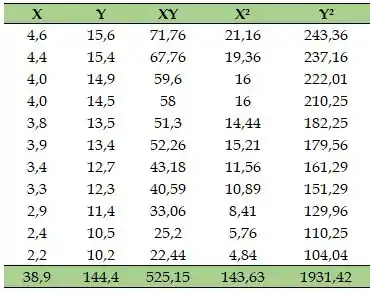
Agora, usando a fórmula do coeficiente de correlação, obtemos:

r = n . ∑ X Y - ∑ X . ∑ Y n . ∑ X 2 - ∑ X 2 . n . ∑ Y 2 - ∑ Y 2 =

11 ∙ 525,15 - 38,9 ∙ 144,4 1 1 ∙ 143,63 - 38,9 ² ∙ 1 1 ∙ 1931,42 - 144,4 ²

r = 0,9 834

Existe uma correlação linear positiva forte entre as variáveis.

Passo 2

(c) Com base no coeficiente de correlação encontrado no problema anterior, r = 0,98 34 , faremos o seguinte teste de hipótese:

H 0 :   ρ = 0   ; H a :   ρ   ≠ 0

Determinando os valores críticos com base na tabela, na significância de 0,05 e nos graus de liberdade g . l .   = n - 2 = 1 1 - 2 = 9 , obtemos:

t =   ± 2,262

A região de rejeição encontra-se abaixo de -2,262 e acima de 2,262.

O valor da estatística t é dado por:

t = r 1 - r ² n - 2 = 0,9 834 1 - 0,98 34 ² 1 1 - 2 = 16,259

Como o valor encontrado está na região de rejeição, 16,259 > 2,262 , então devemos rejeitar a hipótese. Isso é evidência suficiente para que a correlação seja linear.

(d) Vamos encontrar os coeficientes “a” e “b” da reta de regressão linear, que são dados por:

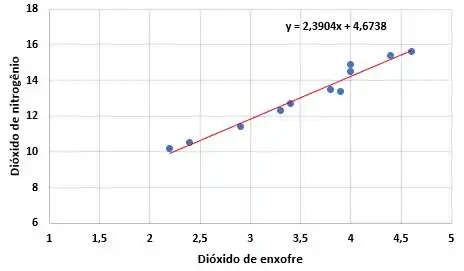
a = ∑ Y ∙ ∑ X 2 - ∑ X ∙ ∑ X ∙ Y n ∙ ∑ X 2 - ∑ X 2 = 144,4 ∙ 143,63 - 38,9 ∙ 525,15 1 1 ∙ 143,63 - 38,9 2 =   4,6738

b = n ∙ ∑ X ∙ Y - ∑ X ∙ ∑ Y n ∙ ∑ X 2 - ∑ X 2 = 1 1 ∙ 525,15 - 38,9 ∙ 144,4 11 ∙ 143,63 - 38,9 2 = 2,3904

Sendo assim, nossa reta de regressão é dada por:

y = a + b x =   4,6738 + 2,3904 x

Tal reta é representada no diagrama de dispersão abaixo:

Passo 3

(e) Sim, pois a reta de regressão linear obtida reforça a constatação de que a correlação linear é forte entre as duas variáveis.

(f) Com base no coeficiente de correlação encontrado r = 0,98 34 , podemos determinar o coeficiente de determinação que é o quadrado do coeficiente de correlação, temos que:

r 2 = 0,98 34 2 = 0,9 671 = 9 6 , 71 %

Isso significa que cerca de 96,71% da variação total entre as variáveis é explicada pela linha de regressão.

Com base nos dados apresentados e com o auxílio do software Excel, obtemos a seguinte tabela de informações, onde Yi representa as aproximações obtidas pela reta de regressão obtida.

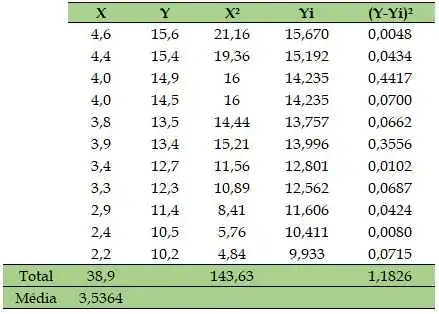
O erro padrão é dado por:

s e = y - y i 2 n - 2 = 1,1826 1 1 - 2 = 0 , 3625    

Espero ter ajudado! Abraços e até a próxima!

Resposta

Consulte os resultados e justificativas acima.