Aplicação de Derivadas

Olá galera!! Sejam muito bem vindos ao Responde Aí, a plataforma de exatas criada para ajudar você a mandar super bem nas suas provas!

Hoje vamos introduzir um assunto bem interessante dentro do cálculo, a aplicação de derivadas.

Nós, alunos de engenharia, matemática, física, e vários outros cursos de exatas, assim que entramos na faculdade nos deparamos com o famoso Cálculo 😮. Nessa disciplina aprendemos basicamente sobre Limites, Derivadas e Integrais.

As vezes a gente fica nas aulas de cálculo se perguntando: “Pra que eu preciso saber dessas coisas?”. Pois hoje vamos te mostrar alguns motivos para aprender e aplicar derivadas.

Algumas aplicações de derivadas são:

1. Calcular taxas de variação instantânea
2. Encontrar máximos e mínimos de uma função
3. Descobrir a concavidade de curvas
4. Esboçar gráficos

E existem muitas outras aplicações para as derivadas. Continua aqui e você vai ver algumas aplicações de derivadas que são super importantes e aparecem em diversos lugares ao longo dos cursos de exatas. Preparado?

Taxas

Podemos calcular taxas de variação instantâneas usando as derivadas.

A própria definição de derivadas nos trás essa aplicação, pois a derivada é entendida como a taxa de variação instantânea da função em relação à variável independente.

Então de maneira geral, podemos definir a taxa de variação de uma função da seguinte maneira:

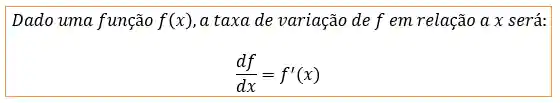
Ou seja, a primeira derivada de uma função é a sua taxa de variação instantânea. Esse cálculo de taxa de variação instantânea é muito útil e vai aparecer em diversas disciplinas.

Onde usamos o cálculo taxas de variação na engenharia?

Na dinâmica temos o cálculo de velocidades pois a velocidade de um objeto é a derivada do deslocamento em relação ao tempo. E também o cálculo de acelerações pois a aceleração de um objeto é a derivada da velocidade em relação ao tempo.

Na ciência dos materiais podemos calcular o fluxo de difusão como a taxa de variação da massa em relação ao tempo.

No estudo de transferência de calor podemos calcular a condução de calor como a taxa de variação da temperatura em relação ao comprimento do corpo.

Ou seja, se você tem uma função que descreve um fenômeno, podemos calcular a taxa de variação dele usando derivadas. Show de bola, não é?

Máximo, mínimo e concavidade

Utilizando as derivadas nós conseguimos encontrar os pontos críticos da função ou seja, o ponto de máximo e o ponto de mínimo de uma função. Dá uma olhada aqui nessa função:

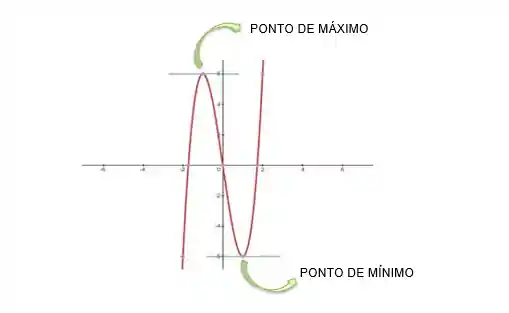
Olhando o gráfico a gente consegue ver claramente qual é o ponto de mínimo e qual é o ponto de máximo. Mas e se você não tiver o gráfico? Como saber onde está o ponto de máximo e de mínimo da função? Usando as derivadas.

Para encontrar os pontos críticos de uma função realize o teste da primeira derivada: calcular a derivar a função e igualar a zero. E assim você encontra os pontos críticos da função.

Beleza, encontrei os pontos críticos, mas como saber qual ponto é de máximo e qual ponto é de mínimo? Pra isso realizamos o teste da segunda derivada: calcule a segunda derivada da equação, aplique o valor do ponto crítico, se for positivo a concavidade é para cima e esse é um ponto de mínimo, se for negativo, a concavidade é pra baixo e é um ponto de máximo

Da uma olhada aqui nesse vídeo sobre taxa

Onde usamos o cálculo de máximo, mínimo e concavidade na engenharia?

Na engenharia definir os pontos de máximo e mínimos são muito importantes no cálculo de funções de custo pois durante um projeto queremos sempre que o custo de produção seja o menor possível.

No estudo de inteligência artificial e em otimização nós utilizamos o cálculo dos pontos de máximos e mínimos para otimizar os modelos matemáticos, pois queremos encontrar o ponto onde o erro do modelo seja minimizado.

Exercício sobre máximos, mínimos e concavidade:

Esboço de Gráficos

Tem como a gente pegar a expressão de uma função e fazer o esboço do gráfico dessa função? SIIIMMM, tem como, e fazemos isso usando as derivadas.

Existe todo um passo a passo para o esboço de gráficos de funções e em muitos desses passos nós utilizamos as derivadas para tirarmos alguma informação, como por exemplo, sabermos quais ou pontos críticos e os pontos de máximo e mínimo, como já comentamos anteriormente.

Ficou curioso? Relaxa que temos uma página que fala só sobre o esboço de gráficos, confere aí: Esboço de Gráficos.

Exercício sobre Esboço de Gráfico

Quer saber mais sobre aplicações de derivadas?

Aqui no Responde Aí nós temos o conteúdo completo que você precisa saber sobre as aplicações de derivadas. E para que seu estudo seja mais focado e rápido nós organizamos todo o conteúdo em capítulos e tópicos. Tudo isso está no nosso Raio-X aqui embaixo 👇🏽

Está esperando o que para conferir? 👇🏽