Espaços Vetoriais

Fala aí, gente bonitaaa!!

Hoje você vai perder o medo de Espaços Vetoriais, ou Espaço Linear!

Se você é o tipo de pessoa que tem pavor de matérias que trabalham só com letras, acha que tudo fica parecendo abstrato e teórico de mais, VEM CÁ, VAMOS SE ABRAÇAR!

Agora, infelizmente não tem muito pra onde fugir, essa matéria é cheia de demonstrações e muito provavelmente a sua prova vai ter questões cheias de letrinhas também! 🥲

Mas fica calmo, agora você tem o RespondeAí! pra te ajudar!

A gente vai começar a aprender sobre espaços vetoriais da mesma forma que a gente aprende a andar de bicicleta. Vamos começar olhando o plano cartesiano que é mais familiar e quando a ideia de espaço vetorial ficar mais palpável a gente vai tirar as rodinhas e ir pro mundo das letrinhas, combinado?!

Ahh, antes da gente começar, só um detalhe! Os espaços vetoriais também são conhecidos como espaços lineares, ok! Então se você ver esse nome por ai, não estranhe!

Agora bora começar!

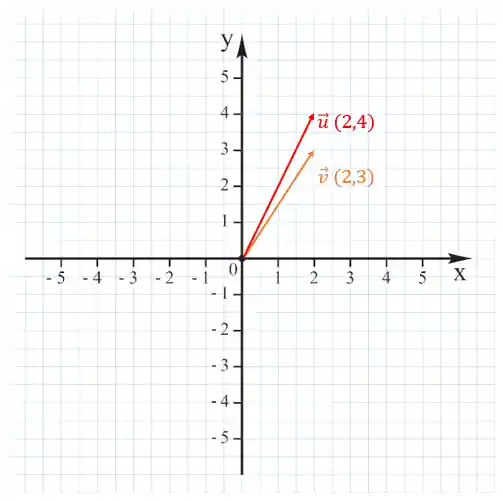
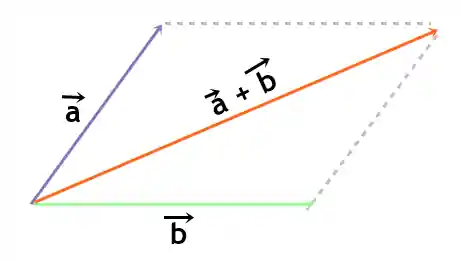
O plano cartesiano é nada mais nada menos que a representação geométrica do espaço vetorial , composto pelas coordenadas assim como o é composto por e por ai vai!

Observando a imagem acima podemos dizer que:

E eles são vetores no espaço vetorial .

Talvez você esteja estranhando que eu não representei os vetores assim e . Como estamos tratando de espaço vetorial é comum omitir essa seta, porque já esta implícito que estamos falando de um vetor. Mas a minha dica é, repara como seu professor ou professora faz e faz igual! 😉

Definição de Espaço Vetorial

Beleza, conseguimos entender o que é a ideia do que é um espaço vetorial. Mas no final das contas, o que define um espaço vetorial?

Para que um conjunto qualquer, representado por seja um espaço vetorial, ele tem que obedecer às seguintes regras:

• Ser um conjunto não vazio;
• Soma:
  • Ou seja, se e são pertencem ao espaço vetorial , então a soma deles também deve pertencer a .
• Multiplicação por um escalar:
  • Ou seja: Seja um escalar, pertencente aos números reais e um vetor de . A multiplicação também pertencerá a

Agora sabemos o que é espaço vetorial, mas não para por ai! Temos axiomas que um espaço vetorial precisa obedecer!

Axiomas da Soma

1. A soma é comutativa

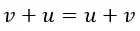
Essa é a famosa “a ordem dos fatores não altera o produto”!

Exemplo: Seja e elementos do com e podemos fazer:

2. A soma é associativa

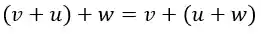
Exemplo: Vamos pegar os elementos , e pertencentes ao e fazer:

3. Elemento neutro da soma

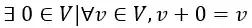
Em outras palavras, existe um vetor nesse espaço vetorial, denotado por , cujo resultado da soma com qualquer outro vetor  do espaço é esse outro vetor .

Exemplo: Vamos pegar o elementos do exemplo anterior e o elemento neutro :

4. Inverso aditivo

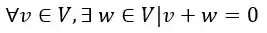
Traduzindo, para todo vetor em , existe um vetor também em , tal que . No universo de operações que conhecemos o inverso aditivo de é o , por exemplo.

Exemplo: Para os elementos e podemos fazer:

Axiomas da Multiplicação por escalar

Agora temos mais axiomas, só que dessa vez relacionados a multiplicação por um escalar! Vamos nessa:

5. Associativo

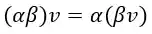
Trata-se do ditado “A ordem dos tratores não altera o viaduto” Não importa se multiplicarmos primeiramente o vetor pelo escalar para depois multiplicar pelo ou os escalares primeiro para depois multiplicar o resultado pelo vetor, o resultado será o mesmo.

Exemplo: Seja , e podemos fazer:

6. Elemento neutro da multiplicação

O elemento neutro é o escalar , cujo resultado da multiplicação dele com qualquer outro vetor do espaço é esse mesmo vetor .

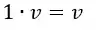
Esse é tão tranquilo que nem precisava de exemplo! Mas vamos lá:

Exemplo:

7. Distributividade 1:

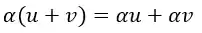
Não se assusta, tem exemplo!

Exemplo: Para os elementos e e o escalar podemos fazer:

8. Distributividade 2

Esse é o último!!!

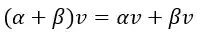
Exemplo: Seja , e podemos fazer:

UFAA!! Acabaram os axiomas! 💃💃💃

São muitos os requisitos que um espaço vetorial deve ter não é mesmo? hahahaha

Agora eu vou te deixar com o nosso conteúdo super irado em vídeo também! Pra você sentir mais o gostinho do RespondeAí! 😉 😋

É isso mesmo, aqui no RespondeAí!, além de textos irados temos vídeos super didáticos. Confere o vídeo de espaços vetoriais aí 👇🏽

Agora, eu preciso te falar uma coisa!

Esse é só o comecinho desse assunto! Então antes de ir embora, confere aqui em baixo o nosso RAIO-X com todo o nosso conteúdo de Espaços vetoriais e Transformações lineares em capítulos e tópicos, tudo bem organizadinho, só esperando por você!👇🏽