Produto Interno

Fala aí! Nós somos o Responde Aí e hoje a gente vai começar a bater um papo sobre Produto Interno!

Antes de qualquer coisa, o produto interno é algo que calculamos entre dois vetores. Então, se temos um dois vetores e , o produto interno entre eles é denotado por:

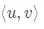
O produto interno é um número real que relaciona o módulo desses vetores e usualmente o calculamos da seguinte maneira: Nós multiplicamos as primeiras coordenadas dos vetores e depois somamos esse resultado com a multiplicação entre as segundas coordenadas dos vetores e assim por diante.

Produto Interno Usual - Exemplo:

Vamos ver um exemplo pra ficar mais claro!

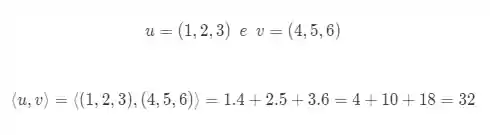
E é agora que entra o mais interessante do produto interno. Nós podemos "inventar" maneiras de calcular esse produto interno. Essa maneira que eu te falei agora é a maneira usual de definir o produto interno e por isso ela tem um nome específico, chamamos de produto escalar.

Mas a gente poderia dizer por exemplo que o produto interno é definido assim:

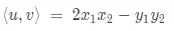
Parece meio loucura isso não é? kkkkk Mas é assim que funciona.

Axiomas do Produto Interno

Só tem mais uma coisinha bem importante que eu preciso te falar: A gente pode definir o produto interno do jeito que quisermos, DESDE QUE, essa definição obedeça aos seguinte axiomas do produto interno

Axioma 1 - Simetria:

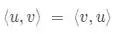
Axioma 2 - Homogeneidade:

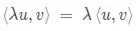
Axioma 3 - Aditividade:

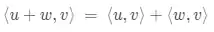
Axioma 4 - Positividade:

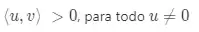
Axioma 5:

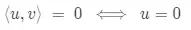
Show de bola? Não esquece disso, estamos combinados? Tem que obedecer a esses axiomas...

Muitas questões sobre produto interno são do seguinte tipo: Eles dão uma definição qualquer de produto interno e querem saber se é realmente uma definição válida, ou seja, se todas os axiomas são obedecidos de modo que a gente possa dizer com certeza que aquela definição é uma definição de produto interno. Então o que temos que fazer é testar esses axiomas para a definição dada e ver se eles são obedecidos, beleza?

Eu vou deixar aqui embaixo 👇🏽 um vídeo que a galera aqui do Responde Aí fez sobre produto interno. Assiste aqui:

Pensando em tudo que você precisa estudar sobre produto interno para arrebentar na prova nós do Responde Aí produzimos todo esse conteúdo e dividimos ele em capítulos e tópicos para o seu estudo ser organizado, rápido e descontraído!

Se liga no no Raio-X aqui embaixo 👇🏽