Análise gráfica
Nos exercícios 13 a 16, um elemento é selecionado aleatoriamente da população representada pelo gráfico. Calcule a probabilidade de que o valor x do elemento pertença ao intervalo correspondente à área sombreada do gráfico. Suponha que a variável x seja normalmente distribuída.
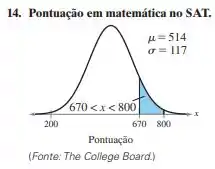
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Antes, vamos pegar aqui as informações que foram dadas no enunciado:
Com isso, vamos calcular o valor do :
Com o valor do , podemos encontrar a área entre os valores:
Podemos então concluir que a probabilidade é: