Enunciado

Probabilidade e Estatística - Probabilidade, um curso moderno com aplicações, de Sheldon Ross- Ed: 8º - Capítulo 1.Problemas - Ex. 7c

E se apenas os garotos sentarem-se juntos?

Passo 1

Opa galeeeeera! Hoje vamos entender mais um pouco sobre o Principio Fundamental da Contagem (PFC).

Aqui temos 3 garotos e 3 garotas e há a restrição de que garotos devem estar agrupados. Então vamos quebrar o problema em 2 partes.

Primeiro vamos descobrir de quantas formas podemos formar o grupo de garotos e depois pensaremos nele como um único indivíduo. E depois vamos calcular de quantas formas podemos colocar as 3 garotas + o grupo de garotos em uma fila de “4” lugares.

Passo 2

Então vamos escolher primeiro como vamos compor o grupo dos garotos. Lembrando do principio fundamental da contagem, toda vez que aparecer um “e” no nosso raciocínio, multiplicaremos as possibilidades de cada um dos casos.

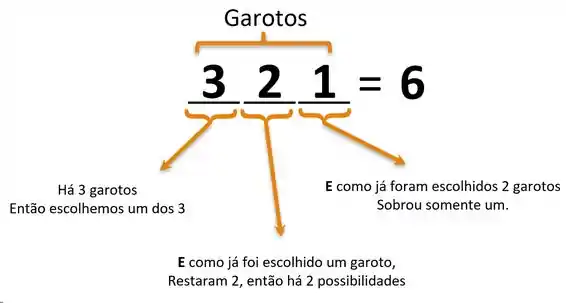
Sendo assim, o grupo “garotos” tem 6 possibilidades.

Passo 3

Agora vamos pensar que temos 3 meninas mais o grupo de garotos, totalizando 4 entidades. Para descobrirmos de quantas formas esse grupo maior pode ser formado, basta descobrirmos a permutação de quatro pessoas.

Temos esse grupo com 24 possibilidades e dentro dele há 6 possibilidades de se formar o grupo de garotos, então o numero total de formas será:

Resposta

3 garotos juntos e 3 garotas podem sentar-se de 144 maneiras diferentes.

Exercícios de Livros Relacionados

Considere um torneio com n competidores no qual o resultado é uma ordenação desses competidores, sendo permitidos empates. Isto é, o resultado divide os jogadores em grupos, com o primeiro grupo sendo

De um grupo de n pessoas, deve-se escolher um comitê de tamanho j. Deste comitê, também será escolhido um subcomitê de tamanho i, i 5 j. (a) Deduza uma identidade combinatória para calcular, de duas m

Seja Hk(n) o número de vetores x1, ... , xk, para os quais cada x, é um inteiro positivo satisfazendo 1 (a) Sem quaisquer cálculos, mostre que H1(n) = sum n Hk-1 Dica: Existem quantos vetores nos quai

Em certa comunidade, há 3 famílias formadas por um único pai e um filho, 3 famílias formadas por um único pai e 2 filhos, 5 famílias formadas por 2 pais e um filho único, 7 famílias formadas por 2 pai

Quantos subconjuntos de tamanho 4 do conjunto S = {1,2, ..., 20) contêm pelo menos um dos elementos l, 2,3,4, 5?