Comparando duas variâncias

Nos exercícios 19 a 26,

(a) identifique a afirmação e formule H0 e Ha,

(b) determine o valor crítico e identifique a região de rejeição,

(c) calcule a estatística de teste F,

(d) decida se rejeita ou não a hipótese nula e

(e) interprete a decisão no contexto da afirmação original.

Suponha que as amostras são aleatórias e independentes e que as populações são normalmente distribuídas. Se for conveniente, use tecnologia.

26. Salários anuais

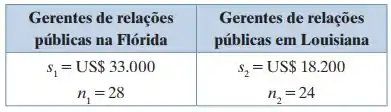
Um serviço de informação sobre emprego afirma que o desvio padrão dos salários anuais para gerentes de relações públicas é maior na Flórida do que em Louisiana. Você seleciona uma amostra de gerentes de relações públicas de cada estado. Os resultados de cada pesquisa são mostrados na tabela a seguir. Para a = 0,05, você pode concordar com a afirmação do serviço? (Adaptado de: America’s Career InfoNet.).

Bom dia, galera!!!! Vamos fazer uma questão de teste de hipótese.

Sejam as variâncias amostrais de duas populações diferentes. Se as duas populações são normais e as variâncias populacionais são iguais, então a distribuição amostral do quociente

é uma distribuição F. A seguir são apresentadas várias propriedades da distribuição F.

1. A distribuição F é uma família de curvas, cada uma determinada por dois tipos de graus de liberdade: os graus de liberdade correspondentes à variância no numerador, denotado por , e os graus de liberdade correspondentes à variância no denominador, denotado por .

2. A distribuição F é positivamente assimétrica.

3. A área total sob cada curva de uma distribuição F é igual a 1.