Construindo e representando graficamente distribuições binomiais Nos exercícios 23 a 26, (a) construa uma distribuição binomial, (b) represente a distribuição binomial usando um histograma e descreva sua forma, e (c) identifique quaisquer valores da variável aleatória x que você consideraria incomuns. Explique seu raciocínio.
25. Desempenho no trabalho Quarenta e seis por cento das mães que trabalham fora dizem que seu desempenho no trabalho é o mesmo de antes de dar à luz. Você seleciona aleatoriamente oito mães que trabalham fora e pergunta como seu desempenho no trabalho mudou desde que deram à luz. A variável aleatória representa o número de mães que trabalham fora que dizem que seu desempenho no trabalho é o mesmo de antes de dar à luz. (Fonte: Forbes.)
Passo 1
Fala galerinha boa, beleza? Questão sobre distribuição binomial.
Para resposta dessa questão, vamos lembrar que n é o tamanho amostral, p é a probabilidade de sucesso e q (1 – p) é a probabilidade de fracasso da distribuição binomial.
A fórmula da distribuição binomial é:
E a fórmula da combinação é:
Passo 2
Primeiramente vamos definir os parâmetros do problema: n = 8; p = 0,46; q = 0,54.
Onde a variável aleatória x é: mães que trabalham fora que dizem que seu desempenho no trabalho é o mesmo de antes de dar à luz.
Passo 3
Na letra (a) para encontrar a distribuição binomial, basta substituir os valores dos parâmetros na fórmula do passo 1. Assim, para cada valor de x, teremos uma probabilidade P(x) associada:
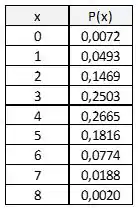
Passo 4
Na letra (b) vamos construir o histograma baseado na tabela de probabilidades da distribuição binomial da letra (a):
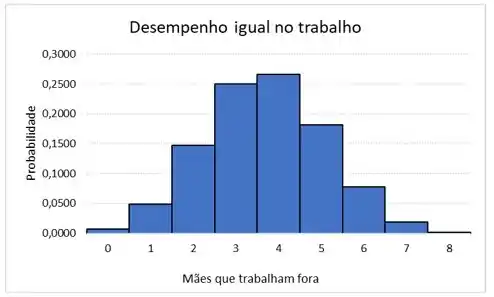
E podemos ver que esse histograma é basicamente simétrico.
Passo 5
Na letra (c) podemos informar que os valores 0, 1, 7 e 8 são incomuns porque suas probabilidades são menores que 0,05.
E é isso galerinha. Até a próxima!
Resposta
Respostas das letras (a), (b) e (c) nos passos acima.