Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 9.Estudo de Caso - Ex. 2i
Correlação entre medidas antropométricas (corporais)
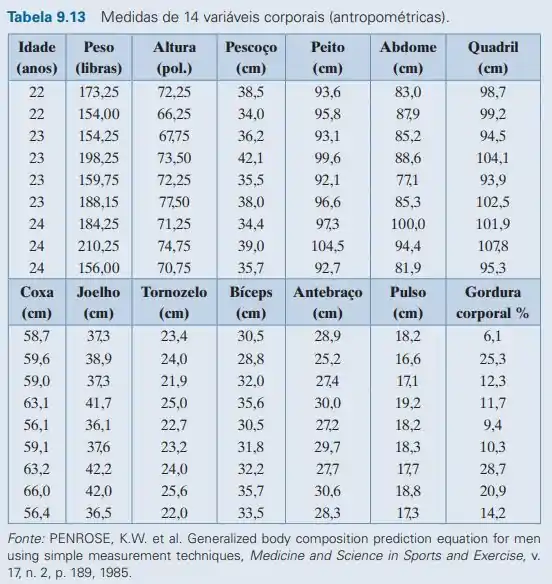
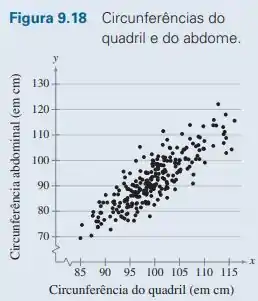
Em um estudo publicado na Medicine and Science in Sports and Exercise (v. 17, n. 2, p. 189) foram tiradas as medidas de 252 homens (idades de 22 a 81 anos). Das 14 variáveis de cada homem, alguns pares têm correlações significativas e outros não. Por exemplo, o diagrama de dispersão na Figura 9.18 mostra que as circunferências do quadril e do abdome dos homens têm uma correlação linear forte (r ≈ 0,874). A Tabela 9.13 mostra somente os dados dos nove primeiros indivíduos.
Agora, use tecnologia para encontrar o coeficiente de correlação para cada par no Exercício 1. Compare seus resultados com aqueles obtidos por intuição.
Item i: (peso, gordura do corpo)
Passo 1
E aí pessoal, belezinha. Vamos com alguns estudos de caso, para entendermos como aplicar os conceitos estudados até agora. Como a questão é meio extensa faremos cada item separadamente, mas seguindo o mesmo procedimento.
Para começar vamos construir a tabela dada no Microsoft Excel:
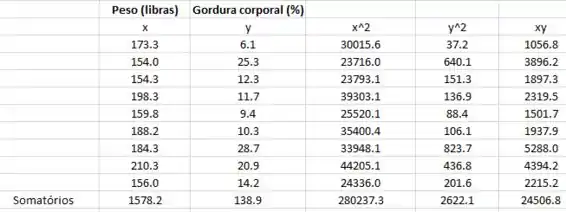
Passo 2
Agora para determinarmos o coeficiente de correlação usaremos a formulação:
Com ajuda da tabela que construímos no Excel, sendo n = 9, vamos substituir os valores e calcular r:
*Observação: Se possível façam os cálculos no Excel para evitar propagação de erros por arredondamentos.
Passo 3
Comparando com a resposta intuitiva, temos que 0,1163 está entre 0,1 e 0,2 satisfazendo uma correlação fraca.
Resposta
Ver passo a passo.