Em um determinado teste de hipótese, a probabilidade de um erro tipo I é fixa, enquanto a probabilidade de um erro tipo II depende do valor particular de usado como alternativa da hipótese nula. Para testes de hipótese do tipo encontrado nesta seção, podemos achar como segue:
Passo 1: Determinar o(s) valo(es) de x que corresponde(m) ao(s) valor(es) crítico(s) em
para substituir Z pelo(s) valor(es) crítico(s), introduzir os valores de e , e resolver em relação a .
Passo 2: Dado um valor particular de que seja uma alternativa da hipótese nula , traçar a curva normal com este novo valor de no centro. Marcar também o(s) valor(es) de achado(s) no Passo 1.
Passo 3: Recorrer ao gráfico do Passo 2 e achar a área da nova região crítica delimitada por . Esta é a probabilidade de rejeitar a hipótese nula quando o novo valor de é correto.
Passo 4: O valor de é 1 menos a área do Passo 3. Esta é a probabilidade de não rejeitar a hipótese nula, quando o novo valor de é correto.
As etapas precedentes permitem-nos achar a probabilidade de não rejeitar quando ela é falsa. Estamos determinando a área sob a curva que exclui a região crítica em que rejeitamos : esta área corresponde a não rejeitarmos uma falsa porque usamos um valor particular de que vai contra . Para o exemplo das temperaturas do corpo humano discutido nesta seção, determine o valor de correspondente a:
a.
b. .
Passo 1
Tudo certo, pessoal? A gente vai fazer agora um exercício que explora um caminho diferente de olhar os testes e hipótese, mas não é nada que não vamos conseguir fazer! Vamos ter que usar uma tabela de distribuição normal de novo! Trouxe aqui uma imagem dela pra vocês!
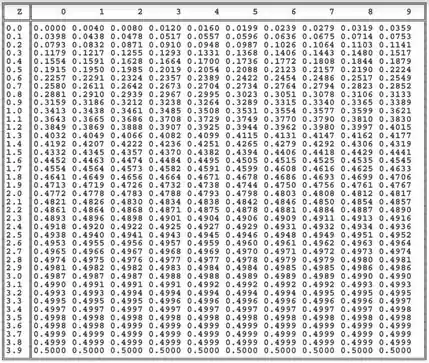
Também vamos precisar usar a fórmula do Z para um Teste de Hipóteses para média (com conhecido ou ):
Primeiro, vamos determinar os valores iniciais do problema. Os dados do exemplo das temperaturas do corpo humano são: , , e .
Percebemos que, para , o valor crítico teria que partir de , ou seja, de um valore da tabela de:
Dessa forma, o valor crítico de Z é: . Logo, seguindo o passo 1 do enunciado:
Show, temos o valor crítico de agora!
Passo 2
Belezinha! Agora vamos ao segundo passo: criar uma curva normal com o valor de no centro. Aqui criaremos um gráfico para a letra A do problema (esquerda) e outro para a letra B (direita). Em seguida, realizaremos o passo 3, demarcando a área da região crítica delimitada por em cada caso. Assim, ficamos com:
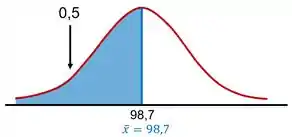
Show! Já temos os dois gráficos que precisávamos! Próximo passo!
Passo 3
Tá quase! Agora, vamos seguir o quarto e último passo para chegar nas respostas:
Sendo assim:
Para a letra A ():
Para a letra B ():
E pronto! Acabamos! Simples, né?
Resposta
a.
b.