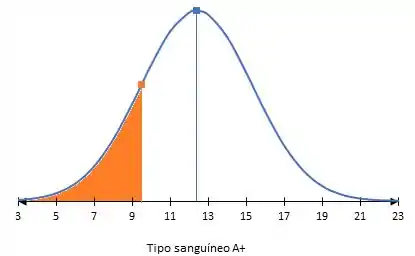
Determine se você pode usar uma distribuição normal para aproximar a distribuição binomial. Se for possível, use a distribuição normal para aproximar as probabilidades indicadas e esboce seus gráficos. Se não for possível, explique o porquê e use a distribuição binomial para encontrar as probabilidades indicadas.
Trinta e um por cento da população dos Estados Unidos têm tipo sanguíneo A+. Você seleciona aleatoriamente 40 pessoas nos Estados Unidos e pergunta se elas têm tipo sanguíneo A+. Encontre a probabilidade de que o número de pessoas que têm tipo sanguíneo A+ seja:
(b) menor que 10
(Fonte: American Association of Blood Banks.)
Passo 1
Olá galerinha! Para este exercício precisamos relembrar algumas regrinhas.
Para calcular uma distribuição normal para aproximar a distribuição binomial, precisamos que e , se essas condições são verdadeiras, então a variável aleatória binomial tem uma distribuição aproximadamente normal, com média:
E desvio padrão:
Onde:
número de tentativa
a probabilidade de sucesso em uma única tentativa
a probabilidade de fracasso em uma única tentativa ()
Passo 2
No exercício temos que:
Logo:
Como e são maiores que 5 então podemos usar a distribuição normal para aproximar a distribuição binomial, para o cálculo da média () e desvio padrão ():
Passo 3
(b) menor que 10
Os valores dos pontos médios discretos são ..., 7, 8, 9. O intervalo que correspondente a distribuição normal contínua é , logo a probabilidade da distribuição normal é
Então iremos encontrar o escore pela seguinte equação:
Onde:
Pela tabela da distribuição normal padrão:
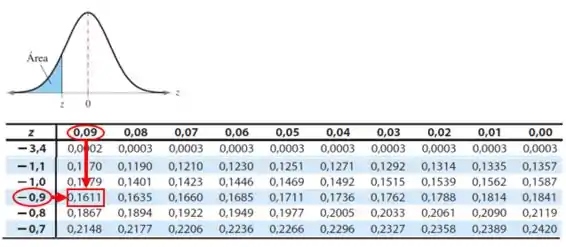
A probabilidade encontrada na tabela é
A probabilidade de que o número de pessoas que têm tipo sanguíneo A+ seja menor que 10 é de 0,1611.