Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 4.3 - Ex. 31

Distribuição de Poisson: variância. Use o fato de que a variância de uma distribuição de Poisson é σ 2 = μ .

Golfe. Em um ano recente, o número médio de tacadas por buraco do jogador de golfe Phil Mickelson era de aproximadamente 3,9.

  1. Calcule a variância e o desvio padrão. Interprete os resultados.
  2. Determine a probabilidade de que ele jogaria uma rodada de 18 buracos e daria mais de 72 tacadas. (Fonte: PGATour.com.)

Passo 1

Oi galerinha, vem comigo!

Pelo enunciado temos:

μ = 3,9 ;

σ 2 = μ .

Então a variância é:

σ 2 = 3,9

E o desvio padrão:

σ = σ 2 = 3,9

σ ≈ 2,0

Passo 2

Para o item (b) precisamos descobrir nosso x :

x > 72 18 > 4

Iremos utilizar a Tabela de Distribuição de Poisson:

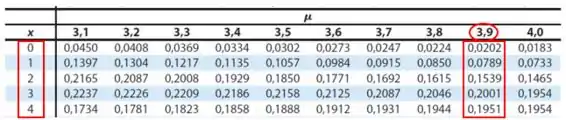
Para determinarmos a probabilidade de que jogaria uma rodada de 18 buracos e daria mais de 72 tacadas. Primeiramente precisamos somar as probabilidades calculadas acima:

P 1 ,   2 ,   3 ,   4 =   0,0202 + 0,0789 + 0,1539 + 0,2001 + 0,1951

P 1 ,   2 ,   3 ,   4 = 0,648

E agora iremos subtrair a soma de 1:

P m a i s   q u e   q u a t r o = 1 - 0,648

P m a i s   q u e   q u a t r o = 0,352

A probabilidade é 0,352 .

Resposta

  1. σ 2 = 3,9 ;

    2. σ ≈ 2,0 .

    A maioria das pontuações de Phil por buraco difere da média por não mais que 2,0 tacadas.

  2. 0,385