Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 9.Revisão - Ex. 9

Nos exercícios 9 a 12, encontre a equação da reta de regressão para os dados. Depois, construa um diagrama de dispersão e represente a reta de regressão. (Cada par de variáveis tem uma correlação significativa). Use a equação de regressão para prever o valor de y para cada um dos valores de x, se apropriado. Se o valor de x não for apropriado para prever o valor de y, explique o porquê. Se for conveniente, use tecnologia.

As quantidades (em bilhões de libras) de leite produzido nos Estados Unidos e os preços médios (em dólares) por galão de leite por nove anos. (Adaptado de: U.S. Department of Agriculture e U.S. Bureau of Labor Statistics).

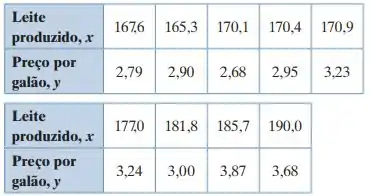
  1. x = 150 bilhões de libras.
  2. x = 175 bilhões de libras
  3. x = 180 bilhões de libras.
  4. x = 210 bilhões de libras

Passo 1

E aí pessoal, belezinha. Vamos com a revisão dos conteúdos de correlação e regressão!!!

Para começarmos, vamos obter a equação da reta de regressão, y ^ = m x + b , a partir da formulação:

m = n ∑ x y - ∑ x ∑ y n ∑ x 2 - ∑ x 2   e   b = ∑ y - m ∑ x n

Para simplificar o processo de resolução, vamos construir uma tabela de dados com o auxílio do Microsoft Excel.

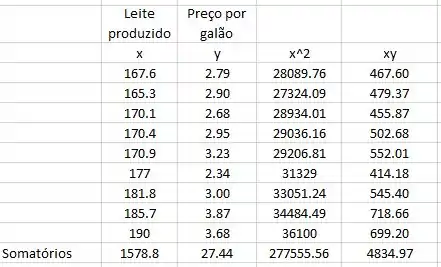
Sabendo que a quantidade de dados é n = 9, e com os valores dos somatórios obtidos, podemos substituir nas fórmulas dadas:

m = 9 ∙ 4834,97 - 1578,8 ∙ 27,44 9 ∙ 277555,56 - 1578,8 2 ≅ 0,0357

e

b = 27,44 - 0,0357 ∙ 1578,8 9 ≅ - 3,2135

Logo, a equação da reta obtida é:

y ^ = 0,0357 x - 3,2135

Passo 2

Após a seleção das colunas dos dados desejados, e a inserção e formatação do gráfico de dispersão (Ver exercício 17 da seção 9.2), teremos:

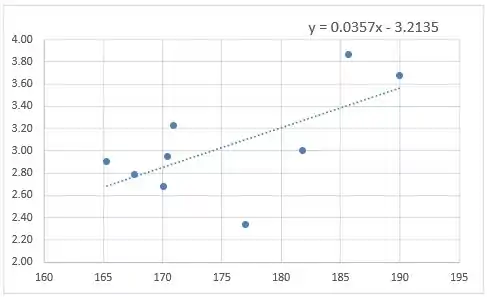
Passo 3

Agora, respondendo cada um dos itens pedidos, teremos:

  1. x = 150 bilhões de libras

    2. Não é apropriado prever o valor de y para x = 150, pois este valor está fora do intervalo de dados observado. Caso a previsão seja feita, será uma extrapolação dos dados, que tem grande chance de incorrer em erro.

  2. x = 175 bilhões de libras

    3. Quando o valor de x é 1450 teremos que y (o preço por galão) é dado por:

    y ^ = 0,0357 ∙ 175 - 3,2135 = 3,034   o u   ≅ 3,0   d ó l a r e s

  3. x = 180 bilhões de libras

    4. De forma similar ao item b, teremos:

    y ^ = 0,0357 ∙ 180 - 3,2135 = 3,2125   o u   ≅ 3,2   d ó l a r e s

  4. x = 210 bilhões de libras

Não é apropriado prever o valor de y para x = 210, pois este valor está fora do intervalo de dados observado. Caso a previsão seja feita, será uma extrapolação dos dados, que tem grande chance de incorrer em erro.

Resposta

Ver passo a passo.