Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.3 - Ex. 17
Nos exercícios 17 a 34, encontre a média, a mediana e a moda dos dados, se possível. Se quaisquer dessas medidas não puderem ser encontradas ou não representarem o centro dos dados, explique o porquê.
17. Créditos da faculdade O número de créditos assumidos por uma amostra de 13 estudantes de tempo integral em uma faculdade para um semestre
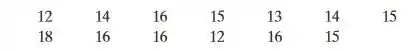
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiramente, vamos entender o conceito de média. A média é a soma de todos os valores dividido quantidade de valores, logo, para este caso, nós vamos ter a seguinte média
Substituindo os valores, nós temos que
Que é aproximadamente
Passo 2
Agora partindo para a mediana, ordenando os valores dos dados do menor para o maior, nós obtemos a seguinte configuração
A mediana é o valor do meio do conjunto de dados classificado, portanto
Já a moda é o valor de dados que ocorre com mais frequência no conjunto de dados. Se não houver valores de dados repetidos, a moda não existe, podemos perceber que o número repete mais vezes, portanto