Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 15.Exercícios propostos - Ex. 1
Um levantamento estatístico feito por um instituto de pesquisa de opinião pública, nas 8 últimas semanas (20/09 a 8/11) que precederam a eleição para senador no estado de São Paulo, em 1974, mostrou os dados do gráfico:
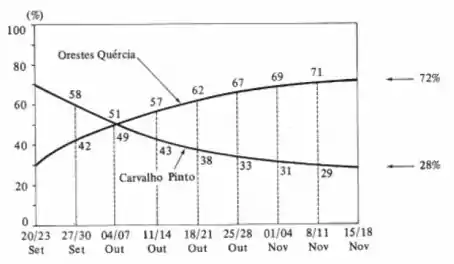
Pede-se:
- Dar a equação da parábola que mostra a evolução da porcentagem de pessoas favoráveis ao candidato vitorioso em função do tempo, e avaliar essa porcentagem em 15/11, comparando-a com a real obtida (71%);
- Idem para o candidato derrotado;
- Calcular o coeficiente de explicação dessas 2 regressões.
Passo 1
Olá galerinha, tudo bem com vocês? Primeiramente iremos relembrar a teoria.
A função polinomial, no caso de ser uma função parabólica (polinômio do 2° grau), tem a seguinte equação:
Quando as variáveis explicativas dependem do tempo, sempre é conveniente, por economia de cálculo e tempo, efetuar a seguinte mudança de variável:
Assim as equações para o cálculo das estimativas da regressão polinomial se reduzem para:
Sabendo disso vamos iniciar nosso exercício colocando os dados do gráfico em tabela, onde:
- tempos;
- candidato vitorioso;
- candidato derrotado.
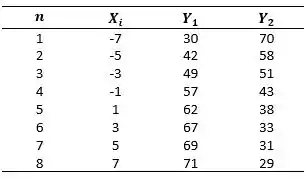
Passo 2
No item a) queremos a equação da parábola do candidato vitorioso:
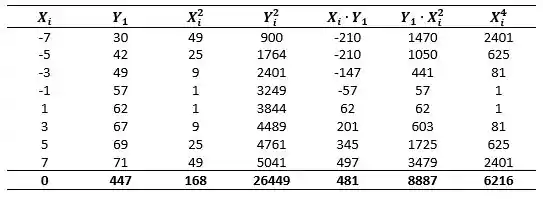
Substituindo no sistema para encontrar os valores de , e :
Resolvendo a equação (3):
Equação (1):
Substituindo na equação (2):
Voltando na equação (1):
A equação da parábola fica:
Considerando que 15/11 é , e substituindo na equação encontrada:
Passo 3
No item b) queremos a equação da parábola do candidato derrotado:
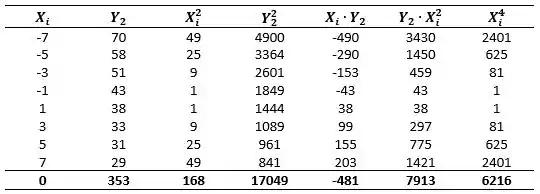
Substituindo no sistema para encontrar os valores de , e :
Resolvendo a equação (3):
Equação (1):
Substituindo na equação (2):
Voltando na equação (1):
A equação da parábola fica:
Considerando que 15/11 é , e substituindo na equação encontrada:
Passo 4
Para o cálculo do coeficiente de explicação, iremos utilizar a seguinte equação:
Onde:
Para o candidato vendedor:
Passo 5
Para o candidato derrotado:
Prontinho pessoal, até mais!
Resposta
- ;
- ;
- .
.
.