Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 15.Problemas - Ex. 7
Obtenha a tabela ANOVA para o Exemplo 15.3, usando o fator regime com os níveis l e 2.
Passo 1
Vamos lá.
Essa é a nossa Tabela 15.3: Perdas de peso de indivíduos submestidos a três regimes.
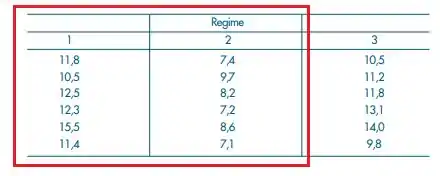
Notem que só vamos usar o fator regime com os níveis 1 e 2 😉.
Logo, temos um teste de comparação entre duas médias. Como qualquer teste de hipótese, a primeira etapa é formular as hipóteses, para uma análise de variância, as hipóteses serão sempre assim:
Agora é partir para os cáculos.
Passo 2
Sabendo que
E calculando
Podemos montar nossa primeira tabelinha
Olhando para as médias amostras, vemos que elas têm valores diferentes, agora precisamos verificar se essa diferença é significativa, ou seja, se nós podemos dizer que baseados nessas diferenças que apareceram nas amostras, as populações são diferentes.
Vamos definir o nível de significância .
Passo 3
Agora, vamos calcular nossas informações que serão agrupadas numa única tabela, conhecida pelo nome de ANOVA, descrita na Tabela a seguir.
Basta aplicarmos as fórmulas que se encontram no Capítulo 10, calculando cada informação, temos
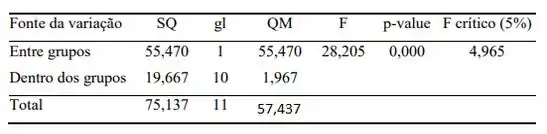
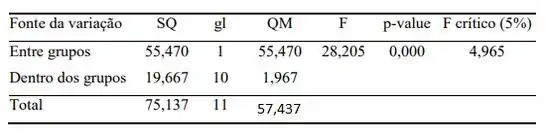
Para não perdemos tempo, que na nossa tabela já constam os valores de F estatístico (28,205), p-valor (0,000) e F crítico (4,965) utilizando um , beleza? 😉
Passo 4
Para finalizarmos, vamos usar a estatística F. Analisando a tabela F: p = 5%, temos que F crítico é igual a 4,96, portanto como F estatístico é maior que F crítico. Rejeitamos , ou seja, existe diferença significativa entre as perdas médias de peso dos regimes 1 e 2.
Resposta
Rejeitamos , ou seja, existe diferença significativa entre as perdas médias de peso dos regimes 1 e 2.