Pontos influentes
Um ponto influente é um ponto no conjunto de dados que pode afetar muito o gráfico de uma reta de regressão. Um outlier pode ou não ser um ponto influente. Para determinar se um ponto é influente, encontre duas retas de regressão: uma incluindo todos os pontos no conjunto de dados e a outra excluindo o possível ponto influente. Se a inclinação ou intercepto em y da reta de regressão mostrar mudanças significativas, então o ponto pode ser considerado influente. Um ponto influente pode ser removido de um conjunto de dados somente quando houver uma justificativa apropriada.
Nos exercícios 35 e 36, (a) construa um diagrama de dispersão dos dados, (b) identifique quaisquer possíveis outliers e (c) determine se o ponto é influente. Explique seu raciocínio.

Passo 1
Item a
E aí pessoal, belezinha. Vamos construir o diagrama de dispersão dos dados fornecidos. Para simplificar o processo de resolução, vamos construir uma tabela de dados com o auxílio do Microsoft Excel.
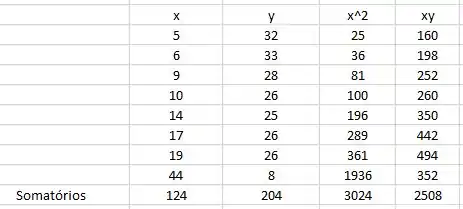
O gráfico de dispersão fica da seguinte forma:
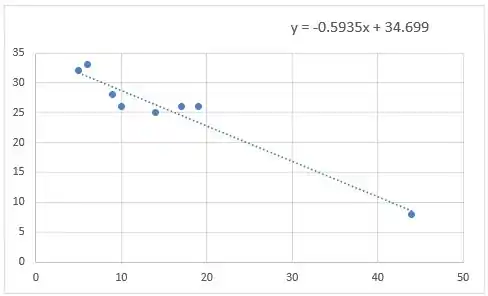
Passo 2
Item b
O ponto mais afastado dos outros é um possível outlier, ou seja, o ponto (44, 8).
Passo 3
Item c
Para averiguarmos se o ponto mencionado é realmente um outlier, vamos construir um novo gráfico de dispersão removendo esse ponto do conjunto de dados utilizado.
Teremos a nova tabela utilizada:
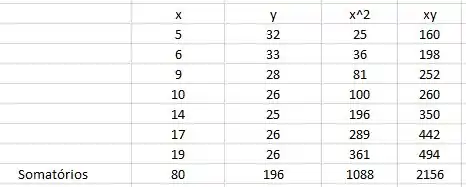
E o novo gráfico de dispersão:
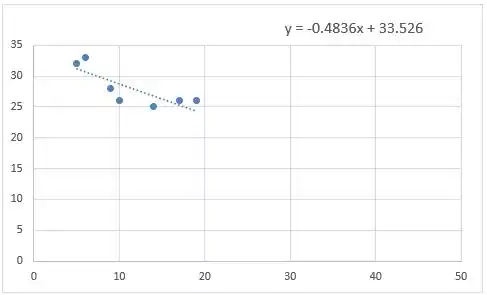
Como os valores dos coeficientes angular (inclinação da reta) e linear (intercepto do eixo vertical) não sofrem alterações drásticas ao removermos o ponto (44, 8), temos que este ponto não é um ponto influente (outlier).
Resposta
Ver passo a passo.