Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 13.Problemas - Ex. 1

Da população X ~ N(50, 100) retirou-se uma amostra casual simples de n = 10 elementos.

Da população Y ~ N(60, 100) retirou-se uma amostra casual simples de m = 6 indivíduos,

independente da primeira. Obtemos as variâncias amostrais S 1 2   e   S 2 2 , respectivamente.

(a) Encontre o valor de a, tal que P S 1 2 S 2 2 < a = 95 % .

(b) Encontre o valor de b, tal que P S 1 2 S 2 2 > b = 95 % .

Passo 1

  Como temos duas populações independentes com distribuição normal, com variâncias populacionais conhecidas a relação entre as variâncias pode ser aproximada por:

F = S 1 2 σ 1 2 S 2 2 σ 2 2 ~ f n 1 - 1 ; m 2 - 1 D i s t r i b u i ç ã o   f   d e   S n e d e c o r ,   c o m   n - 1 n u m e r a d o r   e   m - 1 ( d e n o m i n a d o r )   g r a u s   d e   l i b e r d a d e .

Passo 2

(a) P S 1 2 S 2 2 < a = 95 %

Multiplicando 1 σ 1 2   e   d i v i d i n d o   p o r 1 σ 2 2 :

→ P S 1 2 σ 1 2 S 2 2 σ 2 2 < a . σ 2 2 σ 1 2 = 95 %

Como σ 1 2 = σ 2 2 = 100 :

→ P f 9 ; 5 ≥ a = 5 %

Da tabela de F de Snedecor:

a = 4,77

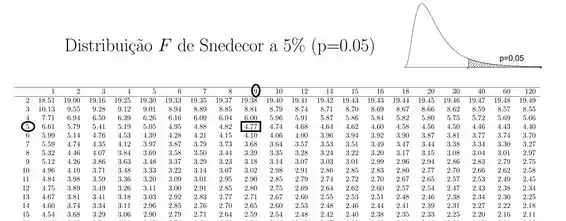
Lembrando que na tabela de F de Snedecor a coluna de cima representa Graus de liberdade do numerador(n-1), e na lateral esquerda os graus de liberdade do denominador(m-1).

Passo 3

(b) P S 1 2 S 2 2 > b = 95 %

Multiplicando 1 σ 1 2   e   d i v i d i n d o   p o r 1 σ 2 2 :

P S 1 2 σ 1 2 S 2 2 σ 2 2 > b . σ 2 2 σ 1 2 = 95 %

P 1 f 5 ; 9 ≤ b = 5 %

Logo b = 0,287

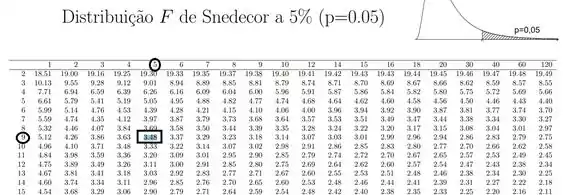
Lembrando que a tabela de Snedecor sempre fornece p para o lado direito, ou seja, quando “ ≥ " ; portanto quando queremos " ≤ " devemos utilizar 1 f m 2 - 1 ; n 1 - 1 (invertemos os graus de liberdade do numerador e denominador).

Resposta

Portanto: a = 4,77   e   b = 0,287

Ver Outros Exercícios desse livro