Há qualquer indicação de que cada fator afete a intensidade de torção? Há qualquer interação entre os fatores? Use
Analise os residuos desse experimento.
Plote a torção média em cada nivel do teor de cobre e compare os niveis usando o método de Fisher. Descreva as diferenças nos efeitos dos diferentes níveis de teor de cobre na torção, se baixa produção fosse desejada. Qual seria o nível do teor de cobre que você específicaria?
Suponha que a temperatura não possa ser facilmente controlada no ambiente entre as placas de cobre estejam sendo usadas. Isso muda a sua resposta dada no item ?
Passo 1
Bom galera, podemos montar uma tabela com os fatores estudados e fica:
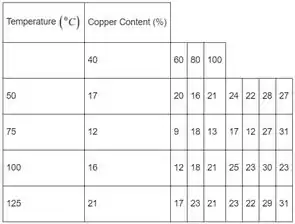
E o modelo é:
As hipóteses devem ser testadas da seguinte forma:
Efeito da temperatura:
Efeito do teor de cobre:
Interação:
Passo 2
Belezinha, montamos a tabela do Minitab colocando os valores do experimento, assim:
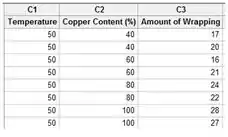
Passo 3
Então, agora fazemos o ANOVA pelo Minitab, e temos como resultado:

Com isso, observamos que o valor da temperatura é que é menor do que o nível de significância . Portando, rejeitamos a hipótese nula e concluímos que a temperatura afeta a intensidade da torção.
Da mesma forma temos que o valor do teor de cobre é que é inferior á . Portanto, rejeitamos a hipótese nula e concluímos que o teor de cobre afeta a intensidade da torção.
E o valor da interação é que é maior do que o nível de significância . Assim, não podemos rejeitar a hipótese nula e concluímos que não temos indicio de interação entres os fatores.
Passo 4
Agora, plotamos os gráficos de probabilidade normal e de resíduos pelo Minitab:
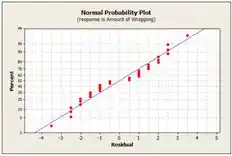
Na primeira temos o gráfico de probabilidade normal dos resíduos. Esse gráfico tem uma linha passando pelo centro, indicando que os residos são normalmente distribuídos.
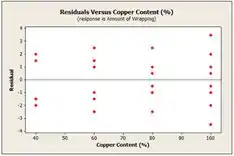
Na segunda e terceira temos os gráficos de resíduos versus dos fatores da temperatura e teor de cobre, respectivamente. A temperatura e o teor de cobre são os que apresentam maiores variabilidades dentro do estudo de cada fator.
E na ultima temos os gráfico de resíduos versus valor ajustado, que não indica nenhum padrão incomum.
Passo 5
Para traçarmos a torção média em cada nível do teor de cobre e coparar os níveis usando o método de Fisher, usamos o software SPSS. E assim temos:
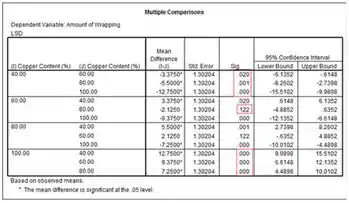
E podemos observar que a quantidade média de torção com e de teor de cobre difere significativamente de todos os outros níveis. No entanto, as quantidades médias de embalagens para e de teor de cobre não diferem significativamente uma das outras.
Podemos também plotar um gráfico da quantidade média de torção em relação aos níveis de teor de cobre, fica:
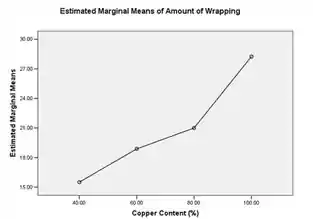
A partir disso, é evidente que a diferença entre a produção média para 60% e 80% do teor de cobre não é significativa. Além disso, mostra que o aumento do teor de cobre aumenta a quantidade média de torção.
Passo 6
Por fim, A partir dos resultados da parte , Sabe se que a interação entre temperatura e teor de cobre não é significativa. Assim , se assumirmos que a temperatura descontrolada e, portanto, fator aleatório, os resultados obtidos na subparte não mudarão.
Resposta
Ei, a resposta está no passo a passo :)