Realizando um teste ANOVA com um fator
Nos exercícios 5 a 14, (a) identifique a afirmação e formule H0 e Ha, (b) determine o valor crítico e identifique a região de rejeição, (c) calcule a estatística de teste F, (d) decida se rejeita ou não rejeita a hipótese nula e (e) interprete a decisão no contexto da afirmação original. Suponha que as amostras são aleatórias e independentes, as populações são normalmente distribuídas e as variâncias populacionais são iguais. Se for conveniente, use tecnologia.
8. Salários do governo
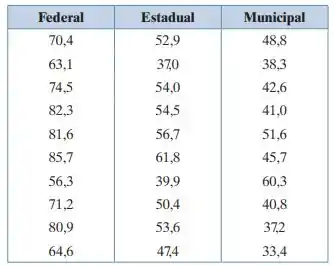
A tabela a seguir mostra os salários (em milhares de dólares) para amostras de pessoas dos níveis de governo federal, estadual e municipal. Para α = 0,01, você pode concluir que pelo menos um salário médio é diferente dos demais? (Adaptado de: Bureau of Labor Statistics.)
Passo 1
Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?
(a) A hipótese nula afirma que todas as médias populacionais são iguais:
A hipótese alternativa afirma o oposto da hipótese nula:
(b) Os graus de liberdade do numerador é o número de grupos k diminuído de 1.
Os graus de liberdade do denominador é o tamanho total da amostra diminuído pelo número de grupos k.
O valor crítico é o valor na linha com e na coluna com da tabela de distribuição F no apêndice do livro com α=0,01. Ou seja, temos:
A região de rejeição contém então todos os valores maiores ou iguais a 5,488.
Passo 2
(c) Com auxílio do Excel e aplicando o teste ANOVA, obtemos os seguintes dados:
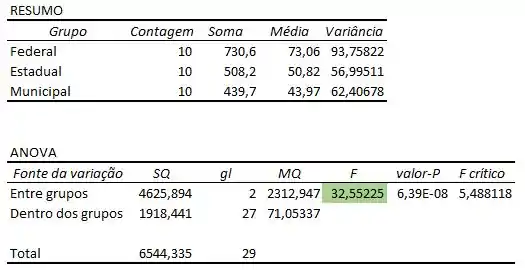
(d) Se o valor da estatística de teste estiver dentro da região de rejeição, então a hipótese nula é rejeitada.
Como:
(e) Há evidências suficientes para apoiar a alegação de que pelo menos um salário médio é diferente dos demais.
Espero ter ajudado! Abraços e até a próxima!

Resposta
Consulte as justificativas acima.