Realizando um teste qui-quadrado para independência

Nos exercícios 13 a 22, realize o teste qui-quadrado para independência indicado fazendo o seguinte:

(a) Identifique a afirmação e declare H0 e Ha.

(b) Determine os graus de liberdade e o valor crítico e identifique a região de rejeição.

(c) Calcule a estatística de teste qui-quadrado. Se for conveniente, use tecnologia.

(d) Decida se rejeita ou não a hipótese nula.

(e) Interprete a decisão no contexto da afirmação original

16. Lesão musculoesquelética

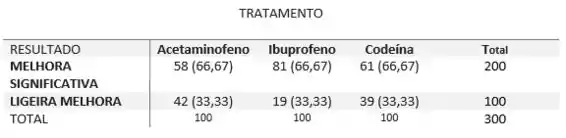
A tabela de contingência a seguir mostra a distribuição de uma amostra aleatória de crianças com dor causada por lesões musculoesqueléticas tratadas com acetaminofeno, ibuprofeno e codeína e o nível de melhora. Com a = 0,10, você pode concluir que o tratamento está relacionado ao resultado? (Adaptado de: American Academy of Pediatrics.)

Bom dia, galera!!!! Vamos fazer uma questão de teste de hipótese.

Um teste qui-quadrado para independência é usado para testar a independência entre duas variáveis. Usando esse teste, você pode determinar se a ocorrência de uma variável afeta a probabilidade de ocorrência da outra variável.

Para realizar um teste qui-quadrado para independência, as seguintes condições devem ser satisfeitas:

1. As frequências observadas devem ser obtidas usando uma amostra aleatória.

2. Cada frequência esperada deve ser maior ou igual a 5. Se essas condições são satisfeitas, então a distribuição amostral para o teste é aproximada por uma distribuição qui-quadrado com

graus de liberdade, em que r e c são os números de linhas e colunas, respectivamente, de uma tabela de contingência. A estatística de teste é:

em que O representa as frequências observadas e E representa as frequências esperadas.