Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.6 - Ex. 17
Refaça o Exercício 16 usando esta aproximação (com k e z dados no Exercício 16):
Passo 1
Fala ae, pessoal! Bora fazer esse exercício!
Neste exercício, vamos utilizar essa nova formula nas condições dadas no Exercício 16. Tanto na letra a quanto na letra b, temos testes bilaterais com . Como o nosso teste é bilateral, temos em cada cauda, então procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.
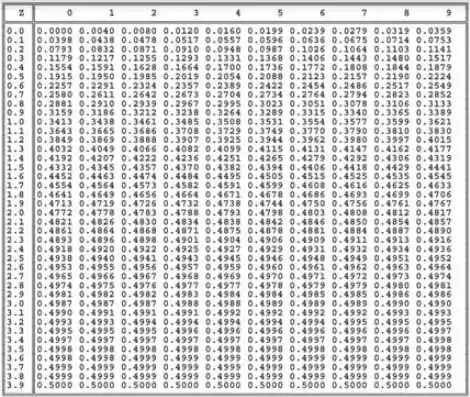
Pela tabela, obtemos o valor crítico:
Passo 2
Agora vamos nos atentar à letra a. Como , temos:
Assim podemos calcular os dois valores críticos.
Usando para encontrar o valor crítico da esquerda, temos:
Usando para encontrar o valor crítico da direita, temos:
Passo 3
Vamos agora ver os valores críticos dados pela tabela da distribuição qui-quadrado.
O valor crítico da esquerda vai ser o valor mostrado na tabela da distribuição qui-quadrado para:
Então, o valor crítico da esquerda vai ser .
E o valor crítico da direita vai ser o valor mostrado na tabela da distribuição qui-quadrado para:
Então, o valor crítico da direita vai ser .
Passo 4
Vamos agora para a letra b. Como , temos:
Assim podemos calcular os dois valores críticos.
Usando para encontrar o valor crítico da esquerda, temos:
Usando para encontrar o valor crítico da direita, temos:
Resposta
a. Utilizando esta nova aproximação, os valores críticos estimados são: 74,216 e 129,565, que são bem próximos dos valores encontrados utilizando a tabela da distribuição qui-quadrado: 74,222 e 129,561.
b. Utilizando esta nova aproximação, os valores críticos estimados são: 117,093 e 184,69.