Rompimento. Vinte e nove por cento dos americanos com idade entre 16 e 21 anos disseram que romperiam com seus namorados ou namoradas por US$ 10.000. Você seleciona aleatoriamente sete pessoas com idade entre 16 e 21 anos. Calcule a probabilidade de que o número de pessoas entre 16 e 21 anos que disseram que romperiam com seus namorados ou namoradas por US$ 10.000 seja:

(b) mais de três.

(Fonte: Bank of America Student Banking & Seventeen.)

Oi galerinha, vamos resolver esse exercício juntos!

Para este exercício iremos utilizar a fórmula da probabilidade binomial. Pelo nosso enunciado temos que:

;

.

Tabela de Distribuição binomial:

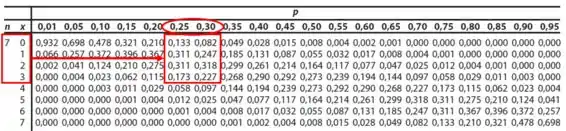
Como na Tabela não temos o valor para , iremos interpolar esses valores:

• Para :



• Para :



• Para :



• Para :

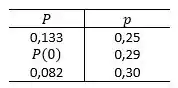
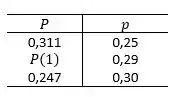
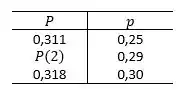
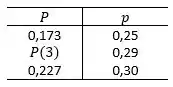
Para determinarmos a probabilidade de que o número de pessoas entre 16 e 21 anos que disseram que romperiam com seus namorados ou namoradas por US$ 10.000 seja mais de três. Primeiramente precisamos somar as probabilidades calculadas acima:

E agora iremos subtrair a soma de 1:

A probabilidade de que mais de três pessoas é .

Espero ter conseguido ajudar, até mais!