A tabela seguinte mostra os resultados de uma pesquisa em que 28.295 adultos foram indagados se eles tiveram um resfriado ou uma gripe no dia anterior. (Adaptado de: Gallup.)

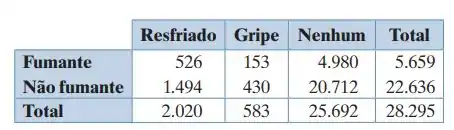
Uma pessoa é selecionada aleatoriamente dessa amostra. Encontre a probabilidade de cada evento:

(a) A pessoa teve resfriado.

(b) A pessoa teve resfriado ou gripe.

(c) A pessoa não teve nenhuma doença, dado que é fumante.

(d) A pessoa não teve nenhuma doença, dado que é não fumante.

(e) A pessoa é fumante, dado que teve gripe.

(f) A pessoa teve gripe ou é não fumante.

(g) A pessoa teve resfriado e é fumante.

Item b

A probabilidade será dada pela soma das duas probabilidades, considerando que ter resfriado e ter gripe são eventos mutuamente exclusivos. Como já calculamos a probabilidade de ter resfriado, vamos calcular a chance de ter gripe, que é dada pelo quociente entre o total de pessoas que tiveram gripe e o total de pessoas da amostra:

A probabilidade de ter resfriado ou ter gripe é dada por:

Item c

Com a condição de ser fumante, o total de pessoas que não tiveram nenhuma doença foi de 4980, em um total de 5659 fumantes. Assim, a probabilidade pedida é de:

Item d

Seguindo o mesmo raciocínio do item anterior, temos um total de 22636 não fumantes, e 20712 não fumantes que não tiveram nenhuma doença. Assim, a probabilidade pedida é:

Item e

Com a condição de que teve gripe, temos um total de 583 pessoas, sendo 153 fumantes que tiveram gripe. Logo, a probabilidade é dada por:

Item f

Como os eventos não são mutuamente exclusivos, pois um não fumante pode ter gripe, teremos que usar a formulação:

Onde sabemos que p(gripe) = 0,0206. Devemos calcular a probabilidade de um indivíduo ser não fumante:

E a probabilidade de ser não fumante e ter tido gripe:

Daí, temos que a probabilidade pedida é dada por:

Item h

O total de indivíduos fumantes que tiveram resfriado é de 526. Logo, a probabilidade pedida é dada por: