A tabela a seguir mostra o número (em milhares) de graus conferidos nos Estados Unidos, por nível e gênero, em um ano recente. (Fonte: U.S. National Center for Education Statistics.)

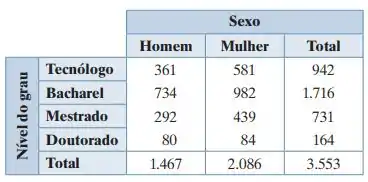
Uma pessoa que obteve grau em um ano recente é selecionada aleatoriamente. Encontre a probabilidade de que essa pessoa seja alguém que:

(a) Obteve grau de bacharel.

(b) Obteve grau de bacharel, dado que a pessoa é mulher.

(c) Obteve grau de bacharel, dado que a pessoa não é mulher.

(d) Obteve grau de tecnólogo ou bacharel.

(e) Obteve grau de doutorado, dado que a pessoa é mulher.

(f) Obteve grau de mestre ou é homem.

(g) Obteve grau de tecnólogo e é homem.

(h) É mulher, dado que obteve grau de bacharel.

Item b

Seguindo o mesmo raciocínio do item anterior, mas atentando-se para a condição dada (Ser mulher), temos que a probabilidade é dada pelo quociente entre a quantidade de mulheres com bacharelado e a quantidade total de mulheres:

Item c

Seguindo o mesmo raciocínio do item anterior, mas atentando-se para a condição dada (Não ser mulher), temos que a probabilidade é dada pelo quociente entre a quantidade de homens com bacharelado e a quantidade total de homens:

Item d

Quando se usa a conjunção ou, temos a probabilidade da união de dois eventos, e o cálculo é dado pela soma das probabilidades individuais em caso de dois eventos mutuamente exclusivos (Que não ocorrem ao mesmo tempo). Como já sabemos a probabilidade de obter o grau de bacharel (item a), devemos calcular a probabilidade de obter o grau de tecnólogo, que será dado pelo quociente entre o total de obtenções desse grau e o total de pessoas do conjunto de dados:

Daí, temos que a probabilidade pedida é dada por:

Item e

Usando o mesmo raciocínio do item b, teremos o quociente entre o total de mulheres que obtiveram o doutorado e o total de mulheres:

Item f

Temos novamente uma união de eventos, mas não conhecemos nenhuma das probabilidades envolvidas. Para cada um dos eventos vamos calcular:

Obter grau de mestre: Quociente entre o total de pessoas que obtiveram o grau de mestre e o total de pessoas do conjunto de dados.

Ser homem: O quociente entre o total de homens e o total de pessoas do conjunto de dados.

Neste item devemos ter o cuidado com os eventos, que não são mutuamente exclusivos, e deveremos subtrair a probabilidade da intersecção dos eventos.

A probabilidade de ser homem e obter grau de mestre é dada pelo quociente entre a quantidade de homens que obtiveram o grau de mestre e o total de pessoas do conjunto de dados:

Daí, temos que a probabilidade pedida é dada por:

Item g

Neste item temos a probabilidade da intersecção de dois eventos, ou seja, que os dois devem ocorrer simultaneamente. Já sabemos do item f, que a probabilidade de ser homem é 0,413 e que a probabilidade de obter o grau de tecnólogo é 0,265 (item d). Logo, a probabilidade pedida é dada por:

Item h

Como temos a condição de ser mulher, mas ter obtido o grau de bacharel, a probabilidade pedida é dada pelo quociente entre o total de mulheres com bacharelado e o total de pessoas com bacharelado, ou seja: