Testando a diferença entre duas médias - Nos exercícios 9 a 20, (a) identifique a afirmação e formule e , (b) encontre o(s) valor(es) crítico(s) e identifique a(s) região(ões) de rejeição, (c) calcule e , (d) calcule a estatística de teste padronizada t, (e) decida se rejeita ou não rejeita a hipótese nula, e (f) interprete a decisão no contexto da afirmação original. Suponha que as amostras são aleatórias e dependentes, e as populações, normalmente distribuídas. Se for conveniente, use tecnologia.
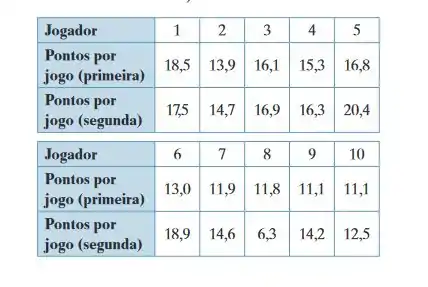
Pontos por jogo - As médias de pontuação (em pontos por jogo) de 10 jogadores profissionais de basquete em suas primeira e segunda temporadas são mostradas na tabela a seguir. Para , há evidência suficiente para concordar com a afirmação de que as pontuações médias mudaram? (Fonte: National Basketball Association.)
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiramente, vamos tabelar a diferença de valor em cada par, com isso, nós temos que
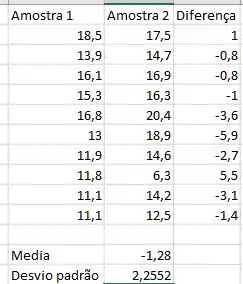
Aqui nós conseguimos duas informações
Passo 2
A – Vamos garantir a seguinte hipótese
B – O valor crítico é o valor dado na tabela 5 com a coluna com grau de liberdade e a coluna sendo (duas caudas), logo
A região de rejeição contém todos os valores menores que e todos os valores maiores que .
C – Nós já temos o resultado, só que em outra notação, com isso,
D – Determinando o valor do teste estatístico,
Substituindo os valores, nós temos que
O que nos dá aproximadamente
E – Se o valor do teste estatístico está na região de rejeição, então a hipótese nula é rejeitada!
F – Não há evidência suficiente para apoiar a alegação.
Resposta
Respondido acima!