Para este teste, faça o seguinte: (a) Identifique a afirmação e formule H0 e Ha. (b) Determine se o teste de hipótese é unilateral à esquerda, unilateral à direita ou bilateral e se deve usar um teste z ou um teste t. Explique seu raciocínio. (c) Encontre o(s) valor(es) crítico(s) e identifique a(s) região(ões) de rejeição. (d) Calcule a estatística de teste padronizada apropriada. Se for conveniente, use tecnologia. (e) Decida se rejeita ou não rejeita a hipótese nula. (f) Interprete a decisão no contexto da afirmação original.
3. Um pesquisador afirma que as concentrações de cobre sérico aumentam em crianças a partir da idade de 7 até 60 dias. A tabela a seguir mostra a concentração de cobre sérico (em microgramas por decilitro) medidas em 12 crianças selecionadas aleatoriamente nas idades de 7 e 60 dias. Para α = 0,05, há evidência suficiente para aceitar a afirmação do pesquisador? Suponha que as populações são normalmente distribuídas. (Adaptado de: U.S. National Library of Medicine.)
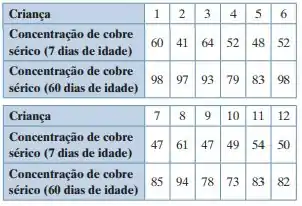
Passo 1
Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?
(a) A partir da afirmação “as concentrações de cobre sérico aumentam em crianças a partir da idade de 7 até 60 dias.”, as hipóteses podem ser definidas como:
(b) Como a hipótese alternativa contém “≠” então o teste é bilateral. Como o desvio padrão populacional é conhecido devemos usar o teste de hipótese z.
(c) Determinando as proporções amostrais, temos:
O valor crítico pode ser encontrado pelo nível de significância na tabela de distribuição normal padrão, assim temos:
A região de rejeição está abaixo de -1,645 e acima de 1,645.
Passo 2
(d) O valor de z é dado por:
(e) Como o valor de z encontrado está abaixo do valor crítico, , devemos rejeitar a hipótese nula.
(f) Isso é o suficiente para rejeitar a afirmação de que as concentrações de cobre sérico aumentam em crianças a partir da idade de 7 até 60 dias.
Espero ter ajudado! Abraços e até a próxima!

Resposta
Isso é o suficiente para rejeitar a afirmação.