Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 10.2 - Ex. 24
Teste de homogeneidade de proporções
Nos exercícios 23 a 26, use a informação a seguir. Outro teste qui-quadrado que envolve uma tabela de contingência é o teste de homogeneidade de proporções. Esse teste é usado para determinar se várias proporções são iguais quando amostras são tiradas de populações diferentes. Antes de as amostras serem selecionadas e as tabelas de contingência construídas, os tamanhos de amostra são determinados. Depois de selecionar aleatoriamente as amostras de populações diferentes, você pode testar se a proporção de elementos em uma categoria é a mesma para cada população usando as mesmas instruções empregadas no teste qui-quadrado para independência. As hipóteses nulas e a alternativa são sempre alguma variação das seguintes afirmações:
H0: as proporções são iguais.
Ha: pelo menos uma proporção é diferente das demais.
Realizar um teste de homogeneidade de proporções requer que as frequências observadas sejam obtidas usando uma amostra aleatória, e cada frequência esperada deve ser maior ou igual a 5.
24. Transtorno obsessivo-compulsivo (TOC)
A tabela de contingência a seguir mostra os resultados de uma amostra aleatória de pacientes com transtorno obsessivo-compulsivo após serem tratados com uma droga ou com um placebo. Para a = 0,10, realize um teste de homogeneidade de proporções na afirmação de que as proporções dos resultados para tratamentos com droga ou placebo são as mesmas. (Adaptado de: The Journal of the American Medical Association.)
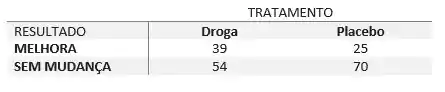
Passo 1
Bom dia, galera!!!! Vamos fazer uma questão de teste de hipótese.
Para realizar um teste qui-quadrado para homogeneidade de proporções, as seguintes condições devem ser satisfeitas:
1. As frequências observadas devem ser obtidas usando uma amostra aleatória.
2. Cada frequência esperada deve ser maior ou igual a 5. Se essas condições são satisfeitas, então a distribuição amostral para o teste é aproximada por uma distribuição qui-quadrado com
graus de liberdade, em que r e c são os números de linhas e colunas, respectivamente, de uma tabela de contingência. A estatística de teste é:
em que O representa as frequências observadas e E representa as frequências esperadas.
Passo 2
Resposta
Rejeita H0. há evidência suficiente, ao nível de significância de 10%, para rejeitar a afirmação de que as proporções dos resultados para tratamentos com droga ou placebo são as mesmas.
Valeu galerinha boa!!!