Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 2.Exercícios - Ex. 24

Use os axiomas para mostrar que, se um evento A estiver contido em outro evento B (ou seja, A é um subconjunto de B ), então P ( A ) ≤ P ( B ) . [Sugestao: neste caso, A e B , A e B ∩ A ' são disjuntos e B = A ∪ ( B ∩ A ' , como pode ser visto em um diagrama de Venn.] Para os A e B genéricos, o que podemos deduzir sobre as relaçoes P ( A ∩ B ) , P ( A ) , e P ( A ∪ B ) ?

Passo 1

Como A está contido em B, então B pode ser escrito como a união de A e (B∩A' ), dois eventos mutuamente exclusivos. (Ver diagrama).

Do axioma  3, P[A\ cup  (B\ capA ') ]= P(A)+P(B\ capA '). Substituindo  P(B) ,

P ( B ) = P ( A ) + P B ∩ A '  or  P ( B ) - P ( A ) = P B ∩ A ' .  Para axioma  1

P B ∩ A ' ≥ 0 ,  então   P ( B ) ≥ P ( A )  ou   P ( A ) ≤ P ( B ) .  Para eventos gerais   A  e   B , P ( A ∩ B ) ≤ P ( A ) e   P ( A ∪ B ) ≥ P ( A )

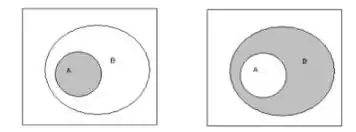
Resposta

A  e   B , P ( A ∩ B ) ≤ P ( A ) e   P ( A ∪ B ) ≥ P ( A )

Exercícios de Livros Relacionados

Sejam três eventos E, F e G. Determine expressões para esses eventos de forma que, de E, F e G, (a) apenas E ocorra; (b) E e G ocorram, mas não F; (c) pelo menos um dos eventos ocorra; (d) pelo menos
Demonstre que P ( E F C )=P ( E )-P ( E F ) .
Se P ( E )=0,9 e P ( F )=0,8 , mostre que P ( E F ) ≥ 0,7 . De forma geral, demonstre a desigualdade de Bonferroni, isto é: P E F ≥ P E + P F - 1
Uma urna contém n bolas vermelhas em bolas azuis. Elas são retiradas uma de cada vez até que um total de r , r ≤ n , bolas vermelhas tenha sido retirado. Determine a probabilidade de que um total de k
Determine a expressão mais simples para os seguintes eventos: (a) ( EUF ) ( EUF C ) ; (b) ( EUF ) ( E CUF ) ( EUF C ) ; (C) ( EUF ) ( FUG )