Você quer estimar o tempo médio que os estudantes universitários gastam assistindo a vídeos on-line a cada dia. A estimativa deve estar dentro do intervalo de 1 minuto da média populacional. Determine o tamanho mínimo de amostra necessário para construir um intervalo de confiança para a média populacional nas condições desejadas. Use o desvio padrão populacional do Exercício 1.

Olá pessoal, vamos relembrar os dados do Exercício 1:

No enunciado diz que a estimativa deve estar dentro do intervalo de 1 min da média populacional, então, temos .

Agora precisamos encontrar o valor crítico () correspondente ao nível de confiança, que iremos considerar como 99% (). Para isso utilizaremos a Tabela de distribuição normal, da seguinte maneira:

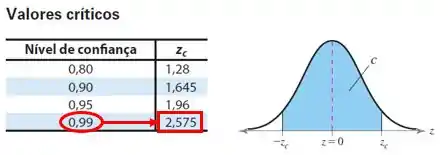
Temos que . Com isso conseguimos calcular o tamanho da amostra ():

Como é decimal, iremos arredondar para o próximo no inteiro, ou seja, .